はじめてのパターン認識

10章

Created by 2GMon

話の流れ

• 距離に基づく手法
  • 非階層的な手法
  • 階層的な手法
• 混合分布に基づく手法
  • 混合正規分布モデル
  • EMアルゴリズム

クラスタリング

データやクラスタ間の類似度に従って、データをいくつかのクラスタにグループ分けする手法

距離

ミンコフスキー距離(1/2)

ユークリッド距離がよく使われるが、ミンコフスキー距離という一般的な距離の定義から様々な 距離を派生させることができる

$N$個ある$d$次元ベクトルの$i$番目を$\boldsymbol{x}_i = (x_{i1}, \ldots , x_{id})^T$ とすると、$\boldsymbol{x}_i$と$\boldsymbol{x}_j$の間のミンコフスキー距離は $$ d(\boldsymbol{x}_i, \boldsymbol{x}_j) = \left( \sum_{k = 1}^d |x_{ik} - x_{jk}|^a \right)^{1/b} $$

$a$は特徴間の差に対する重みを調整するパラメータ $$ 2^1 : 10^1 = 2 : 10, \;\; 2^2 : 10^2 = 4 : 100 $$

$b$は特徴間の差の和に対する重みを調整するパラメータ $$ 4^{1/1} : 100^{1/1} = 4 : 100, \;\; 4^{1/2} : 100^{1/2} = 2 : 10 $$

ミンコフスキー距離(2/2)

• マンハッタン距離：$a=1, b=1$の場合 $$ d(\boldsymbol{x}_i, \boldsymbol{x}_j) = \sum_{k = 1}^d |x_{ik} - x_{jk}| $$
• ユークリッド距離：$a=2, b=2$の場合 $$ d(\boldsymbol{x}_i, \boldsymbol{x}_j) = \left( \sum_{k = 1}^d |x_{ik} - x_{jk}|^2 \right)^{1/2}$$
• ユークリッド距離の2乗：$a=2, b=1$の場合 $$ d(\boldsymbol{x}_i, \boldsymbol{x}_j) = \sum_{k = 1}^d |x_{ik} - x_{jk}|^2 $$
• チェビシェフ距離：$a = b = \infty$の場合 $$ d(\boldsymbol{x}_i, \boldsymbol{x}_j) = \lim_{a \rightarrow \infty} \left( \sum_{k = 1}^d |x_{ik} - x_{jk}|^a \right)^{1/a} = \max_k |x_{ik} - x_{jk}| $$

その他の距離

K-means法(1/5)

$N$個の$d$次元データを、データ間の類似性を尺度に、予め定めた$K$個のクラスタに分類する手法

K-means法(2/5)

各クラスタの代表ベクトルの集合を$\cal{M} = \{\boldsymbol{\mu}_1 , \ldots , \boldsymbol{\mu}_k\}$、$k$番目の代表ベクトルが支配するクラスタを$M(\boldsymbol{\mu}_k)$、$i$番目のデータが $M(\boldsymbol{\mu}_k)$に帰属するか表す帰属変数を $ q_{ik} = \left\{\begin{array}{ll} 1 & (\boldsymbol{x}_i \in M(\boldsymbol{\mu}_k)) \\ 0 & otherwise \end{array} \right. $ とし、K-means法の評価関数 $$ J(q_{ik}, \boldsymbol{\mu}_k) = \sum_{i = 1}^N \sum_{k = 1}^K q_{ik} || \boldsymbol{x}_i - \boldsymbol{\mu}_k || ^2 $$ を最小化する$q_{ik}, \boldsymbol{\mu}_k$が求める結果

K-means法(3/5)

$\boldsymbol{\mu}_k$に関する最適化は以下のようになるので $$ \frac{\partial J(q_{ik}, \boldsymbol{\mu}_k)}{\partial \boldsymbol{\mu}_k} = 2 \sum_{i = 1}^N q_{ik} (\boldsymbol{x}_i - \boldsymbol{\mu}_i) = 0 \Rightarrow \boldsymbol{\mu}_k = \frac{\sum_{i = 1}^N q_{ik} \boldsymbol{x}_i}{\sum_{i = 1}^N q_{ik}} $$ 代表ベクトルは、クラスタに帰属するベクトルの平均ベクトル

K-means法(4/5)

$\boldsymbol{\mu}_k$に関する最適化を$q_{ik}$と同時に最適化するのは難しいので、 逐次最適化を行う

K-means法(5/5)

この最適化アルゴリズムは初期値依存

代表ベクトルは平均ベクトルなので一般にデータベクトルと一致しないが、代表ベクトルを データベクトルに限った方法をK-medoids法という

K-means法はデータ間の距離が定義出来なければ計算できないが、K-medoids法は データ間の非類似度行列が定義できれば計算できる

medoidは$i = \arg \min_{\boldsymbol{x}_i \in M(\boldsymbol{\mu}_k)} \sum_{\boldsymbol{y} \in \{M(\boldsymbol{\mu}_k) - \boldsymbol{x}_i\}} d(\boldsymbol{x}_j, \boldsymbol{y})$ を満たす $\boldsymbol{x}_j$で、距離の1乗で 誤差が評価されるので、2乗のK-means法よりも外れ値の影響が少ない

階層型クラスタリング

$N$個のデータを類似度の高い順に融合して大きなクラスタを作り、 最終的に1つのクラスタに統合する手法

データを融合する仮定はデンドログラムと呼ばれる木構造で表現でき、 デンドログラムを見ることで良いクラスタに分割できる

単連結法(最短距離法)

クラスタ$A, B$間で最も類似度の高いデータ間の距離をクラスタ間の距離にする方法 $$d(A, B) = \min_{\boldsymbol{x} \in A, \boldsymbol{y} \in B} d(\boldsymbol{x}, \boldsymbol{y})$$

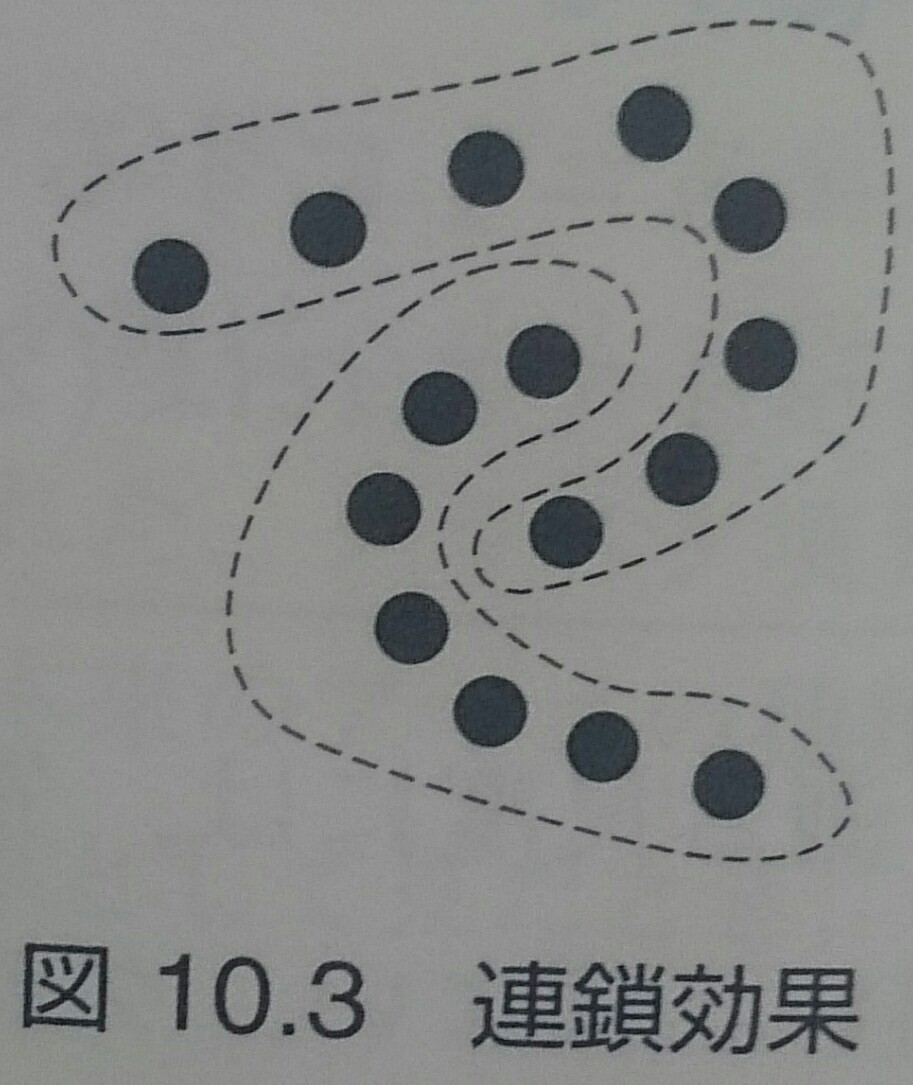
完全連結法(最長距離法)

クラスタ$A, B$間で最も類似度の低いデータ間の距離をクラスタ間の距離にする方法 $$d(A, B) = \max_{\boldsymbol{x} \in A, \boldsymbol{y} \in B} d(\boldsymbol{x}, \boldsymbol{y})$$

• 大きなクラスタができにくく、同じようなサイズのクラスタができる傾向
• 連鎖効果が現れない

郡平均法

クラスタ$A, B$間で最も類似度の低いデータ間の距離をクラスタ間の距離にする方法 $$d(A, B) = \frac{1}{N_A N_B} \sum_{\boldsymbol{x} \in A, \boldsymbol{y} \in B} d(\boldsymbol{x}, \boldsymbol{y})$$

Ward法

クラスタ$A, B$を融合した時のクラスタ内変動の増加分をクラスタ間の距離にする方法 $$ \begin{align} d(A, B) & = \sum_{\boldsymbol{x} \in A, B} d(\boldsymbol{x}, \boldsymbol{\mu}_{AB})^2 - \left(\sum_{\boldsymbol{x} \in A} d(\boldsymbol{x}, \boldsymbol{\mu}_A)^2 + \sum_{\boldsymbol{x} \in B} d(\boldsymbol{x}, \boldsymbol{\mu}_B)^2 \right) \\ & = S_{AB} - (S_A + S_B) \end{align}$$

確率モデルによるクラスタリング

K-means法や階層型クラスタリングでは、1つのデータは1つのクラスタのみに分類される

データ分布に確率モデルを当てはめ、属するクラスタを確率的に決める手法もある

多くの確率モデルは単峰性の確率分布しか表現できないので、 複数の確率モデルの重み付き線形和で全体の確率分布をモデル化する

クラスタ数$K$、$k$番目のクラスタの確率モデル$p_k(\boldsymbol{x})$、重み$\pi_k$ として、全体の確率分布を表す $$ p(\boldsymbol{x}) = \sum_{k = 1}^K \pi_k p_k(\boldsymbol{x}) $$

混合正規分布モデル

$k$番目のクラスタを表す$d$次元正規分布関数を $$ \mathcal{N}(\boldsymbol{x}|\boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k) = \frac{1}{(2\pi)^{1/d} |\boldsymbol{\Sigma}|^{1/2}} \exp \left(- \frac{1}{2} (\boldsymbol{x} - \boldsymbol{\mu}_k)^T \boldsymbol{\Sigma}_k^{-1} (\boldsymbol{x} - \boldsymbol{\mu}_k) \right) $$ とすると、全体の分布はこれらの線形和になる $$ p(\boldsymbol{x}) = \sum_{k = 1}^K \pi_k \mathcal{N}(\boldsymbol{x}|\boldsymbol{\mu}_k, \boldsymbol{\Sigma}), \;\; 0 \leq \pi_k \leq 1, \;\; \sum_{k = 1}^K \pi_k = 1 $$

パラメータは $$ \boldsymbol{\pi} = (\pi_1, \ldots , \pi_K), \; \boldsymbol{\mu} = (\boldsymbol{\mu}_1, \ldots , \boldsymbol{\mu}_K), \; \boldsymbol{\Sigma} = (\boldsymbol{\Sigma}_1, \ldots , \boldsymbol{\Sigma}) $$ で、$\boldsymbol{\mu}_k$は$d$次元ベクトル、$\boldsymbol{\Sigma}_k$は$d \times d$対角行列で $(d + 1) d / 2$個の異なる要素を持つので、全体で $K + dK + (d + 1) d K / 2$個のパラメータを求める必要がある

隠れ変数と事後確率(1/2)

混合正規分布モデルのパラメータを推定するために、1つのデータがどのクラスタに属するか 推定する必要があり、属するクラスタを表現するために$K$次元の変数を用いる $$\boldsymbol{z} = (z_1, \ldots , z_K)^T, \;\; \sum_{k = 1}^K z_k = 1, \;\; \boldsymbol{z} = (0, \ldots , 0, 1, 0, \ldots , 0)^T $$ この変数は、観測される変数$\boldsymbol{x}$が所属する隠れたクラスタを指定しているので、 隠れ変数と呼ばれる

隠れ変数と事後確率(2/2)

$ p(\boldsymbol{x} | z_k = 1) = \mathcal{N}(\boldsymbol{x} | \boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k)$なので、 観測データの隠れ変数による条件付き分布は $p(\boldsymbol{x} | \boldsymbol{z}) = \prod_{k = 1}^K \left( \mathcal{N}(\boldsymbol{x} | \boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k) \right)^{z_k}$

$p(z_k = 1) = \pi_k$なので、隠れ変数の分布は $ p(\boldsymbol{z}) = \prod_{k = 1}^K \pi_k^{z_k} $

$p(\boldsymbol{x})$は同時分布$p(\boldsymbol{x}, \boldsymbol{z})$を全ての$\boldsymbol{z}$ について加えると求まるので $$ p(\boldsymbol{x}) = \sum_{k = 1}^K p(\boldsymbol{z}) p(\boldsymbol{x}|\boldsymbol{z}) = \sum_{k = 1}^K \prod_{k = 1}^K \pi_k^{z_k} \prod_{k = 1}^K ( \mathcal{N}(\boldsymbol{x} | \boldsymbol{\mu}_k, \Sigma_k))^{z_k} = \sum_{k = 1}^K \pi_k \mathcal{N}(\boldsymbol{x}|\boldsymbol{\mu}_k , \boldsymbol{\Sigma}_k) $$

よって、隠れ変数の事後確率は以下のように表せる $$ \begin{align} p(z_k = 1 | \boldsymbol{x}) & = \frac{p(z_k = 1) p(\boldsymbol{x} | z_k = 1)}{p(\boldsymbol{x})} = \frac{p(z_k = 1) p(\boldsymbol{x} | z_k = 1)}{\sum_{j = 1}^K p(z_j = 1) p(\boldsymbol{x} | z_j = 1)} \\ & = \frac{\pi_k \mathcal{N}(\boldsymbol{x} | \boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k)}{ \sum_{j = 1}^K \pi_j \mathcal{N}(\boldsymbol{x} | \boldsymbol{\mu}_j, \boldsymbol{\Sigma}_j)} \end{align} $$

完全データの対数尤度(1/2)

観測データは$N$個あるので、隠れ変数も$N$組ある

観測データを$\boldsymbol{X} = (\boldsymbol{x}_1, \ldots, \boldsymbol{x}_N), \;\; \boldsymbol{x}_i = (x_{i1}, \ldots, x_{id})^T$、 隠れ変数を $\boldsymbol{Z} = (\boldsymbol{z}_1, \ldots, \boldsymbol{z}_N), \;\; \boldsymbol{z}_i = (z_{i1}, \ldots, z_{id})^T$と表し、観測データと隠れ変数を合わせた集合 $$ \boldsymbol{Y} = (\boldsymbol{x}_1, \ldots , \boldsymbol{x}_N, \boldsymbol{z}_1, \ldots , \boldsymbol{z}_N) = (\boldsymbol{X}, \boldsymbol{Z}) $$ を完全データという

混合正規分布モデルのパラメータは、完全データの尤度を最大にするパラメータ

完全データの対数尤度(2/2)

完全データの尤度は $$ \begin{align} p(\boldsymbol{Y}|\boldsymbol{\pi}, \boldsymbol{\mu}, \boldsymbol{\Sigma}) & = p(\boldsymbol{Z}|\boldsymbol{\pi}, \boldsymbol{\mu}, \boldsymbol{\Sigma}) p(\boldsymbol{X}|\boldsymbol{Z}, \boldsymbol{\pi}, \boldsymbol{\mu}, \boldsymbol{\Sigma}) \\ &= \prod_{i = 1}^N \prod_{k = 1}^K ( \pi_k \mathcal{N}(\boldsymbol{x}_i|\boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k) )^{z_{ik}} \end{align} $$

対数尤度は $$ \begin{align} \tilde{\mathcal{L}} & = \ln p(\boldsymbol{Y}|\boldsymbol{\pi}, \boldsymbol{\mu}, \boldsymbol{\Sigma}) = \sum_{i = 1}^N \sum_{k = 1}^K z_{ik} \ln \pi_k + ^sum_{i = 1}^N \sum_{k = 1}^K z_{ik} \ln \mathcal{N}(\boldsymbol{x}_i|\boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k) \\ & = \sum_{i = 1}^N \sum_{k = 1}^K z_{ik} \ln \pi_k \\ & \;\;\; + \sum_{i = 1}^N \sum_{k = 1}^K z_{ik} ( -\frac{d}{2} \ln (2\pi) + \frac{1}{2} \ln |\boldsymbol{\Sigma}_k|^{-1} - \frac{1}{2}(\boldsymbol{x}_i - \boldsymbol{\mu}_k)^T \boldsymbol{\Sigma}_k^{-1} (\boldsymbol{x}_i - \boldsymbol{\mu}_k) ) \end{align}$$

隠れ変数があるので、最尤推定値を直接求めることは出来ない

Q関数

完全データの対数尤度の隠れ変数に関する期待値は $$ \begin{align} \mathcal{L} & = E_z\{ \tilde{\mathcal{L}} \} = \sum_{i = 1}^N \sum_{k = 1}^K E_{z_{ik}} \{ z_{ik} \} \ln \pi_k \\ & \;\;\; + \sum_{i = 1}^N \sum_{k = 1}^K E_{z_{ik}} \left( - \frac{d}{2} \ln (2\pi) + \frac{1}{2} \ln |\boldsymbol{\Sigma_k}|^{-1} - \frac{1}{2}(\boldsymbol{x}_i - \boldsymbol{\mu}_k)^T \boldsymbol{\Sigma}_k^{-1} (\boldsymbol{x}_i - \boldsymbol{\mu}_k) \right) \end{align} $$

隠れ変数に関する期待値は、隠れ変数の事後確率となる $$ E_{z_{ik}} \{ z_{ik} \} = \sum_{z_{ik} = \{0, 1\}} z_{ik} p(z_{ik}|\boldsymbol{x}_i, \pi_k, \boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k) = 1 \times p(z_{ik} = 1 | \boldsymbol{x}_i) $$

隠れ変数の期待値を事後確率で置き換えた関数をQ関数という $$ \begin{align} Q & = \sum_{i = 1}^N \sum_{k = 1}^K p(z_{ik} = 1 | \boldsymbol{x}_i) \ln \pi_k \\ & \;\;\; + \sum_{i = 1}^N \sum_{k = 1}^K p(z_{ik} = 1 | \boldsymbol{x}_i) \left( - \frac{d}{2} \ln (2\pi) + \frac{1}{2} \ln |\boldsymbol{\Sigma_k}|^{-1} - \frac{1}{2}(\boldsymbol{x}_i - \boldsymbol{\mu}_k)^T \boldsymbol{\Sigma}_k^{-1} (\boldsymbol{x}_i - \boldsymbol{\mu}_k) \right) \end{align} $$

EMアルゴリズム(1/9)

隠れ変数がある場合に、確率モデルのパラメータの最尤推定値を求める手法

ExpectationステップとMaximizationステップで構成される

Expectationステップでは確率モデルのパラメータを固定して隠れ変数の事後確率を求め、 MaximizationステップではEステップで求めた隠れ変数の事後確率をQ関数に代入して、 Q関数を最大にするパラメータを求める

EステップとMステップを、完全データの対数尤度に変化がなくなるまで繰り返すことで、 パラメータの最尤推定値を得る

収束地は初期値に依存するので局所最適解に陥る場合がある

EMアルゴリズム(2/9)

EMアルゴリズム(3/9)

Mステップは、Q関数を各パラメータで微分して0と置くことで導出できる

$k$番目のクラスタに属するデータ数の推定値は、 隠れ変数の事後確率を全てのデータについて加えれば $N_k = \sum_{i = 1}^N p(z_{ik}|\boldsymbol{x}_i)$ により得られる

EMアルゴリズム(4/9)

$\boldsymbol{\mu}_k$の最尤推定値は、 Q関数を$\boldsymbol{\mu}_k$で微分して0とおけば $$ \begin{align} \frac{\partial Q}{\partial \boldsymbol{\mu}_k} & = - \frac{\partial}{\partial \boldsymbol{\mu}_k} \left( \sum_{i = 1}^N \sum_{k = 1}^K p(z_{ik}|\boldsymbol{x}_i) \frac{1}{2} (\boldsymbol{x}_i - \boldsymbol{\mu}_k)^T \boldsymbol{\Sigma}_k^{-1} (\boldsymbol{x}_i - \boldsymbol{\mu}_k) \right) \\ & = - \sum_{i = 1}^N p(z_{ik}|\boldsymbol{x}_i) \sum_k^{-1} (\boldsymbol{x}_i - \boldsymbol{\mu}_k) = 0 \end{align} $$ より、次のようになる $$ \boldsymbol{\mu}_k = \frac{1}{N_k} \sum_{i = 1}^N p(z_{ik}|\boldsymbol{x}_i) \boldsymbol{x}_i $$

EMアルゴリズム(5/9)

$\boldsymbol{\Sigma}_k$の最尤推定値は、Q関数を共分散行列の逆行列で微分して0とおけば $$ \begin{align} \frac{\partial Q}{\partial \boldsymbol{\Sigma}_k^{-1}} & = \frac{\partial}{\partial \boldsymbol{\Sigma}_k^{-1}} \left( \sum_{i = 1}^N \sum_{k = 1}^K p(z_{ik}|\boldsymbol{x}_i) \left( \frac{1}{2} \ln |\boldsymbol{\Sigma}_k|^{-1} - \frac{1}{2} (\boldsymbol{x}_i - \boldsymbol{\mu}_k)^T \boldsymbol{\Sigma}_k^{-1} (\boldsymbol{x}_i - \boldsymbol{\mu}_k) \right) \right) \\ & = \sum_{i = 1}^K p(z_{ik}|\boldsymbol{x}_i) \left( \frac{1}{2} \frac{\partial \ln |\boldsymbol{\Sigma}_k^{-1}|}{ \partial \boldsymbol{\Sigma}_k^{-1}} - \frac{1}{2} \frac{\partial \mathtt{Tr} \left( \boldsymbol{\Sigma}_k^{-1} (\boldsymbol{x}_i - \boldsymbol{\mu}_k) (\boldsymbol{x}_i - \boldsymbol{\mu}_k)^T \right)}{ \partial \boldsymbol{\Sigma}_k^{-1}} \right) \\ & = \frac{1}{2} \sum_{i = 1}^N p(z_{ik}|\boldsymbol{x}_i) \boldsymbol{\Sigma}_k - \frac{1}{2} \sum_{i = 1}^N p(z_{ik}|\boldsymbol{x}_i) (\boldsymbol{x}_i - \boldsymbol{\mu}_k) (\boldsymbol{x}_i - \boldsymbol{\mu}_k)^T = 0 \end{align}$$ より、次のようになる $$ \boldsymbol{\Sigma}_k = \frac{\sum_{i = 1}^N p(z_{ik}|\boldsymbol{x}_i) (\boldsymbol{x}_i - \boldsymbol{\mu}_k) (\boldsymbol{x}_i - \boldsymbol{\mu}_k)^T}{ N_k} $$

EMアルゴリズム(6/9)

混合比には$\sum_{k = 1}^K \pi_k = 1$という制約があるので、ラグランジュ関数 $f = \sum_{i = 1}^N \sum_{k = 1}^{K} p(z_{ik}|\boldsymbol{x}_i) \ln_{\pi_k} + \lambda \left( \sum_{k = 1}^{K} \pi_k - 1 \right)$を微分して0とおけば $$ \frac{\partial f}{\partial \pi_k} = \frac{1}{\pi_k} \sum_{i = 1}^{N} p(z_{ik}|\boldsymbol{x}_i) + \lambda = 0 \Rightarrow \pi_k = - \frac{1}{\lambda} \sum_{i = 1}^{N} p(z_{ik}|\boldsymbol{x}_i) $$ となり、 $$ \frac{\partial f}{\partial \lambda} = \sum_{i = 1}^{N} \pi_k - 1 = 0 \Rightarrow - \frac{1}{\lambda} \sum_{k = 1}^{K} \sum_{i = 1}^{N} p(z_{ik}|\boldsymbol{x}_i) = 1 $$ が成り立つので $$ - \frac{1}{\lambda} = \frac{1}{ \sum_{k = 1}^{K} \sum_{ i = 1 }^{ N } p(z_{ik}|\boldsymbol{x}_i) } = \frac{ 1 }{ \sum_{ k = 1 }^{ K } N_k } = \frac{ 1 }{ N } $$ より $$ \pi_k = \frac{ \sum_{ i = 1 }^{ N } p(z_{ik}|\boldsymbol{x}_i) }{ N } = \frac{ N_k }{ N } $$

EMアルゴリズム(7/9)

確率モデルのパラメータが$ \boldsymbol{ \theta } $のとき、観測データ $ \boldsymbol{ X } $ の尤度は、隠れ変数$ \boldsymbol{ Z } $ を含めて表現すれば $$ p( \boldsymbol{ X } | \boldsymbol{ \theta } ) = \frac{ p( \boldsymbol{ X }, \boldsymbol{ Z } | \boldsymbol{ \theta } ) }{ p( \boldsymbol{ Z } | \boldsymbol{ X }, \boldsymbol{ \theta } ) } $$ なので、 $ \boldsymbol{ Z } $ に関する任意の分布$ q( \boldsymbol{ Z })$ に対して、 観測データの対数尤度は $$ \begin{align} \ln{ p( \boldsymbol{ X } | \boldsymbol{ \theta } ) } & = \sum_{ \boldsymbol{ z } } q( \boldsymbol{ Z } ) \ln{ p( \boldsymbol{ X } | \boldsymbol{ \theta } ) } = \sum_{ \boldsymbol{ z } } \ln{ \frac{ p( \boldsymbol{ X }, \boldsymbol{ Z } | \boldsymbol{ \theta } ) }{ p( \boldsymbol{ Z } | \boldsymbol{ X }, \boldsymbol{ \theta } ) } } \\ & = \sum_{ \boldsymbol{ z } } q( \boldsymbol{ Z } ) \ln{ \left( \frac{ p( \boldsymbol{ X }, \boldsymbol{ Z } | \boldsymbol{ \theta } ) }{ q ( \boldsymbol{ Z } ) } \frac{ q ( \boldsymbol{ Z } ) }{ p( \boldsymbol{ Z } | \boldsymbol{ X }, \boldsymbol{ \theta } ) } \right) } \\ & = \sum_{ \boldsymbol{ z } } \ln{ \frac{ p( \boldsymbol{ X }, \boldsymbol{ Z } | \boldsymbol{ \theta } ) }{ q ( \boldsymbol{ Z } ) } } + \sum_{ \boldsymbol{ z } } q( \boldsymbol{ Z }) \ln{ \frac{ q ( \boldsymbol{ Z } ) }{ p( \boldsymbol{ Z } | \boldsymbol{ X }, \boldsymbol{ \theta } ) } } \end{align} $$

EMアルゴリズム(8/9)

第1項を$ \mathcal{ L } ( q, \boldsymbol{ \theta } ) $、第2項を $ \mathtt{ KL }(q || p) $ と置くと $$ \ln{ p( \boldsymbol{ X } | \boldsymbol{ \theta } ) } = \mathcal{ L } (q, \boldsymbol{ \theta }) + \mathtt{ KL }(q || p) $$ と書ける

$ \mathtt{ KL } $ は $ q( \boldsymbol{ Z } ) $ と事後分布 $ p( \boldsymbol{ Z } | \boldsymbol{ X }, \boldsymbol{ \theta } ) $ の間の カルバック-ライブラー情報量とよばれる確率分布間の距離を与える量で、正の値を取る

よって、$ \mathcal{ L } ( q, \boldsymbol{ \theta } ) $ は、観測データの 対数尤度 $ \ln p( \boldsymbol{ X } | \boldsymbol{ \theta } ) $ の下限を与えていることになる

EMアルゴリズム(9/9)

EMアルゴリズムは $ \ln p( \boldsymbol{ X } | \boldsymbol{ \theta } ) $ を 逐次最大化する

Eステップは$t$回目で求めた $ \boldsymbol{ \theta }^{(t)} $ を固定して、 $ \mathcal{ L } ( q, \boldsymbol{ \theta } ) $ を $q$に関して最大化する

Mステップは最大化された $q^{(t)}$を用いて、$ \mathcal{ L } ( q, \boldsymbol{ \theta } ) $ を $ \boldsymbol{ \theta } $ に関して最大化することで、 $ \mathtt{ KL }(q || p) $ を小さくし、隠れ変数の分布を真の分布に近づける