はじめてのパターン認識
8章
Created by 2GMon
話の流れ
- 線形分離可能なときのSVM
- 線形分離不可能なときのSVM
サポートベクトルマシン
最大マージンを実現する2クラス問題の線形識別関数学習法
不等式制約条件下で最適化問題を解くことでマージン最大化を得る
線形分離不可能な場合はスラック変数を導入することで誤り最小の線形識別関数を得られる
非線形特徴写像で高次元非線形特徴空間に写像して線形分離可能にすることもできる
多クラスの場合は一対多SVMにすることが多い
導出(1/14)
クラスラベル付き学習データ集合$D_L = \{(t_i, {\bf x}_i)\} \;\; (i = 1, \ldots , N, \;\; t_i = \{ -1, +1 \}\;$教師データ$, {\bf x}_i \in {\bf \cal{R}}^d$ 学習データ $)$
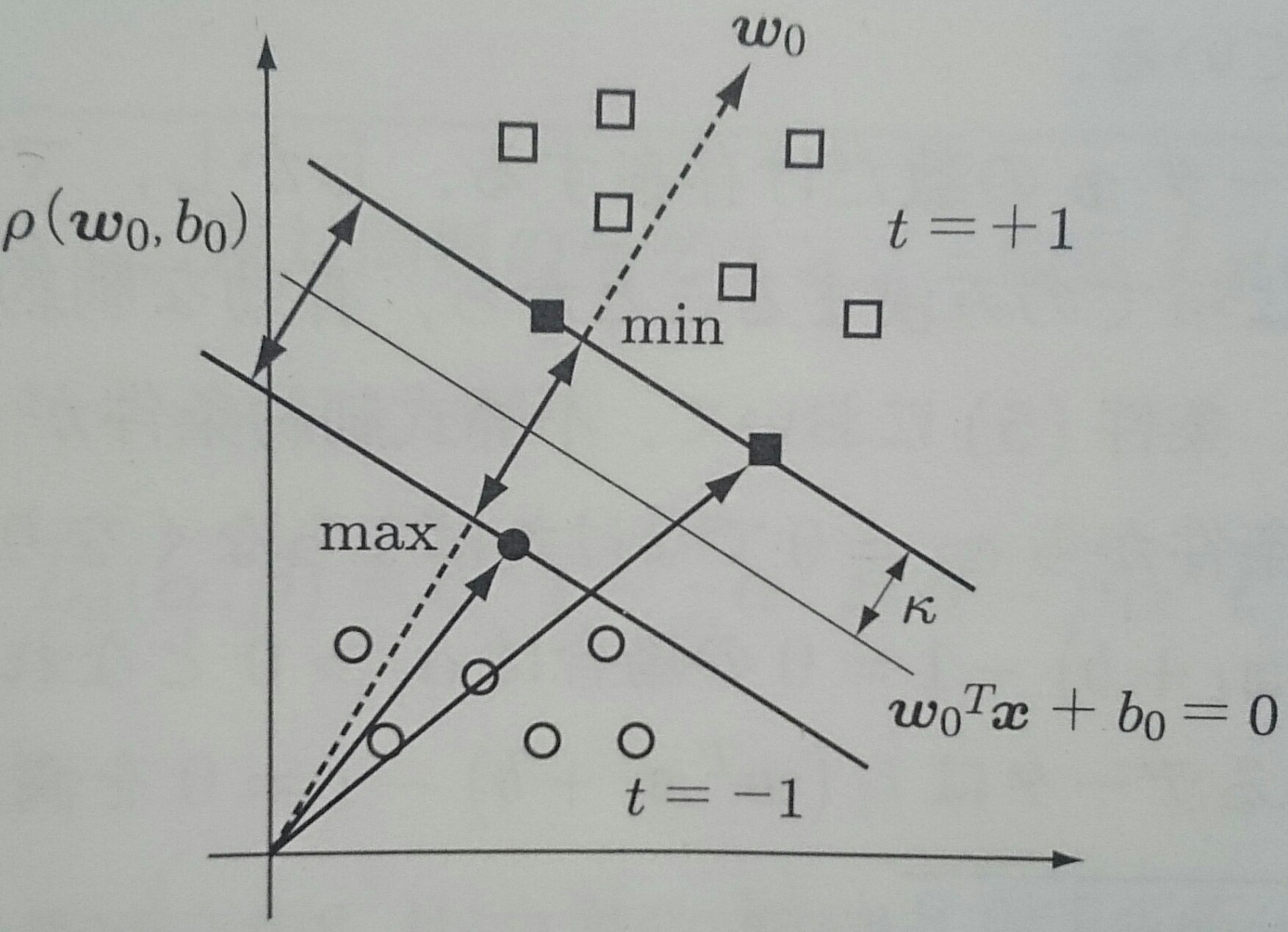
線形識別関数のマージンを$\cal{k}$とすれば、全ての学習データで $$ |\textbf{$\omega$}^T {\bf x}_i + b| \geq \cal{k}$$ が成り立ち、 係数ベクトルとバイアス項を$\kappa$で正規化すると $$ t_i (\textbf{$\omega$}^T {\bf x}_i + b) \geq 1 $$
導出(2/14)
クラス間マージンは、データを$\textbf{$\omega$}$の方向へ射影した長さの差の最小値で $$ \begin{align} \rho (\textbf{$\omega$}, b) & = \min_{{\bf x} \in C_{y = +1}} \frac{\textbf{$\omega$}^T {\bf x}}{||\textbf{$\omega$}||} - \max_{{\bf x} \in C_{y = -1}} \frac{\textbf{$\omega$}^T {\bf x}}{||\textbf{$\omega$}||} = \frac{1 - b}{||\textbf{$\omega$}||} - \frac{-1 - b}{||\textbf{$\omega$}||} \\ & = \frac{2}{||\textbf{$\omega$}||} \end{align} $$ 最適な超平面を$\textbf{$\omega$}_0^T {\bf x} + b_0 = 0$とすれば、この超平面は 最大クラス間マージン $$\rho (\textbf{$\omega$}_0, b_0) = \max_{\textbf{$\omega$}} \rho(\textbf{$\omega$}, b)$$ を与える
導出(3/14)
最大マージン$D_{max}$は最大クラス間マージンの$1/2$なので、最適識別超平面は $t_i(\textbf{$\omega$}^T {\bf x}_i + b) \geq 1$の制約のもとで$\textbf{$\omega$}$の ノルムを最小にする解 $$ \textbf{$\omega$}_0 = \min ||\textbf{$\omega$}|| $$ として求められる
$t_i(\textbf{$\omega$}^T {\bf x}_i + b) \leq 1$の制約のもとで、 ノルム最小の係数ベクトルを求める問題は、正則化項と同じ働きをする
導出(4/14)
マージン最大化の最適識別超平面は、以下の不等式制約条件最適化問題の主問題を解くことで得られる
評価関数(最小化) $$ L_p(\textbf{$\omega$}) = \frac{1}{2} \textbf{$\omega$}^T \textbf{$\omega$} $$ 不等式制約条件 $$t_i(\textbf{$\omega$}^T {\bf x}_i + b) \geq 1 $$
導出(5/14)
この不等式制約条件最適化問題は以下のラグランジュ関数として定式化される $$ \widetilde{L}_p (\textbf{$\omega$}, b, \textbf{$\alpha$}) = \frac{1}{2} \textbf{$\omega$}^T \textbf{$\omega$} - \sum_{i = 1}^N \alpha_i (t_i(\textbf{$\omega$}^T {\bf x}_i + b) - 1) \\ (\textbf{$\alpha$} = (\alpha_1 , \cdots , \alpha_N)^T\;\; \alpha_i \geq 0) $$
$\alpha_i$をラグランジュ未定乗数という
導出(6/14)
この最適化問題の解$\textbf{$\omega$}_0$と$b_0$は以下のKKT条件を満たす解として得られる
- $ \frac{\partial \widetilde{L}_p(\textbf{$\omega$}, b, \textbf{$\alpha$})}{\partial \textbf{$\omega$}} |_{\textbf{$\omega$}=\textbf{$\omega$}_0} = \textbf{$\omega$}_0 - \sum_{i = 1}^N \alpha_i t_i {\bf x}_i = 0 $
- $\frac{\widetilde{L}_p (\textbf{$\omega$}, b, \textbf{$\alpha$})}{\partial b} = \sum_{i = 1}^N \alpha_i t_i = 0 $
- $t_i(\textbf{$\omega$}^T {\bf x}_i + b) - 1 \geq 0$
- $\alpha_i \geq 0$
- $\alpha_i(t_i(\textbf{$\omega$}^T {\bf x}_i + b) - 1) = 0$
導出(7/14)
条件5($\alpha_i(t_i(\textbf{$\omega$}^T {\bf x}_i + b) - 1) = 0$)は相補性条件と呼ばれ、不等式制約条件が有効か否かの判断を与える
条件3($t_i(\textbf{$\omega$}^T {\bf x}_i + b) - 1 \geq 0$)はデータ${\bf x}$の数だけ存在するが、マージンは識別超平面に最も近いデータによってのみきまるので、有効な条件はそのデータによるもののみ
条件5において
- $t_i(\textbf{$\omega$}^T {\bf x}_i + b) - 1 > 0$の場合、 相補性条件から$\alpha_i = 0$になり、制約は無効になる
- $t_i(\textbf{$\omega$}^T {\bf x}_i + b) - 1 = 0$の場合、 $\alpha_i > 0$なので、制約は有効になる
導出(8/14)
KKT条件1($ \frac{\partial \widetilde{L}_p(\textbf{$\omega$}, b, \textbf{$\alpha$})}{\partial \textbf{$\omega$}} |_{\textbf{$\omega$}=\textbf{$\omega$}_0} = \textbf{$\omega$}_0 - \sum_{i = 1}^N \alpha_i t_i {\bf x}_i = 0 $) より、最適解は $$ \textbf{$\omega$}_0 = \sum_{i = 1}^N \alpha_i t_i {\bf x}_i $$ と表せるので、最適解は有効な不等式制約条件をもつ学習データの線型結合となる
導出(9/14)
最適解とKKT条件2 ($\frac{\widetilde{L}_p (\textbf{$\omega$}, b, \textbf{$\alpha$})}{\partial b} = \sum_{i = 1}^N \alpha_i t_i = 0 $)とラグランジュ関数 $$ \widetilde{L}_p (\textbf{$\omega$}, b, \textbf{$\alpha$}) = \frac{1}{2} \textbf{$\omega$}^T \textbf{$\omega$} - \sum_{i = 1}^N \alpha_i (t_i(\textbf{$\omega$}^T {\bf x}_i + b) - 1) $$ より、 ラグランジュの未定乗数のみの関数 $$ \begin{align} L_d(\textbf{$\alpha$}) & = \frac{1}{2} \textbf{$\omega$}_0^T \textbf{$\omega$}_0 - \sum_{i = 1}^N \alpha_i t_i \textbf{$\omega$}^T {\bf x}_i - b \sum_{i = 1}^N \alpha_i t_i + \sum_{i = 1}^N \alpha_i \\ & = \sum_{i = 1}^N \alpha_i - \frac{1}{2} \textbf{$\omega$}_0^T \textbf{$\omega$}_0 = \sum_{i = 1}^N \alpha_i - \frac{1}{2} \sum_{i = 1}^N \sum_{j = 1}^N \alpha_i \alpha_j t_i t_j {\bf x}_i^T {\bf x}_j \end{align} $$ が得られる
導出(10/14)
KKT条件1($ \frac{\partial \widetilde{L}_p(\textbf{$\omega$}, b, \textbf{$\alpha$})}{\partial \textbf{$\omega$}} |_{\textbf{$\omega$}=\textbf{$\omega$}_0} = \textbf{$\omega$}_0 - \sum_{i = 1}^N \alpha_i t_i {\bf x}_i = 0 $) より、最適解が$\textbf{$\omega$} = \sum_{i = 1}^N \alpha_i t_i {\bf x}_i$のように 学習データの線型結合で表現されることから、係数$\alpha_i$を求める問題に置き換えられる
最適な$\alpha_i$は $$ \begin{align} L_d(\textbf{$\alpha$}) & = \frac{1}{2} \textbf{$\omega$}_0^T \textbf{$\omega$}_0 - \sum_{i = 1}^N \alpha_i t_i \textbf{$\omega$}^T {\bf x}_i - b \sum_{i = 1}^N \alpha_i t_i + \sum_{i = 1}^N \alpha_i \\ & = \sum_{i = 1}^N \alpha_i - \frac{1}{2} \textbf{$\omega$}_0^T \textbf{$\omega$}_0 = \sum_{i = 1}^N \alpha_i - \frac{1}{2} \sum_{i = 1}^N \sum_{j = 1}^N \alpha_i \alpha_j t_i t_j {\bf x}_i^T {\bf x}_j \end{align} $$ を最大にする$\textbf{$\alpha$}$により得られる
これを主問題に対する双対問題という
導出(11/14)
$N$個の1を並べたベクトルを${\bf 1} = (1, \ldots, 1)^T$、学習データで作られた行列を $ H = (H_{ij} = t_i t_j {\bf x}_i^T {\bf x}_j) $、教師ベクトルを ${\bf t} = (t_1, \ldots , t_N)^T$とすれば、双対問題は以下のように表現される
評価関数(最大化) $$ L_d(\textbf{$\alpha$}) = \textbf{$\alpha$}^T {\bf 1} - \frac{1}{2} \textbf{$\alpha$}^T {\bf H} \textbf{$\alpha$} $$ 制約条件 $$ \textbf{$\alpha$}^T {\bf t} = 0 $$
導出(12/14)
双対問題のラグランジュ関数$\widetilde{L}_d(\textbf{$\alpha$})$は、 ラグランジュ未定乗数を$\beta$とすれば、 $$ \widetilde{L}_d(\textbf{$\alpha$}, \beta) = \textbf{$\alpha$}{\bf 1} - \frac{1}{2} \textbf{$\alpha$}^T {\bf H} \textbf{$\alpha$} - \beta \textbf{$\alpha$}^T {\bf t} $$ KKT条件5($\alpha_i(t_i(\textbf{$\omega$}^T {\bf x}_i + b) - 1) = 0$)より、 $\alpha_i(t_i(\textbf{$\omega$}^T {\bf x}_i + b) - 1) = 0$がすべての $i = 1, \ldots , N$ で成り立てばいい
導出(13/14)
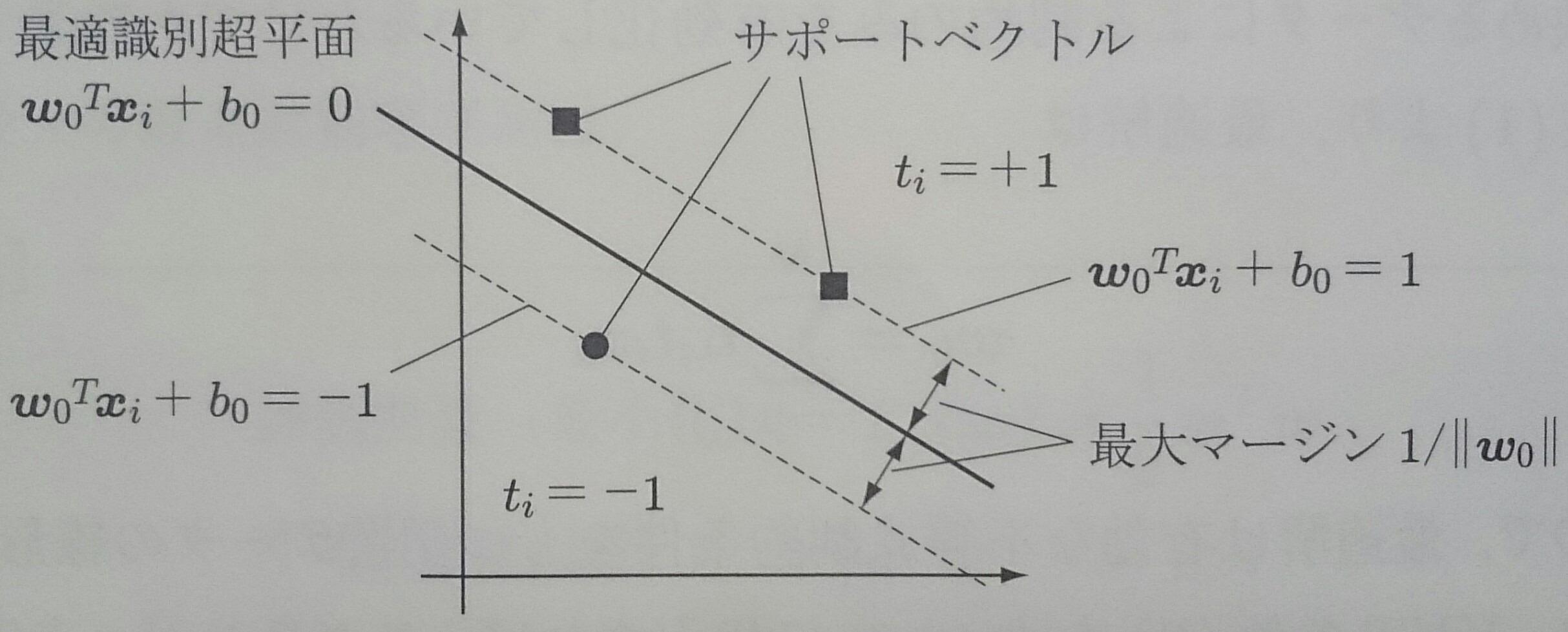
$$ \left\{ \begin{array}{ll} t_i (\textbf{$\omega$}^T {\bf x}_i + b) - 1 = 0 & \alpha_i > 0 \\ t_i (\textbf{$\omega$}^T {\bf x}_i + b) - 1 \neq 0 & \alpha_i = 0 \\ \end{array} \right. $$ $\alpha_i > 0$となる${\bf x}_i$をサポートベクトルといい、最適識別超平面を構成する要素となる
導出(14/14)
最適なバイアス$b_0$はサポートベクトルの一つ${\bf x}_s$を用いて $t_s(\textbf{$\omega$}_0^T {\bf x}_s + b_0) - 1 = 0$ を解いて求める
ラグランジュ乗数の最適解を $\widetilde{\textbf{$\alpha$}}=(\widetilde{\alpha}, \ldots , \widetilde{\alpha}_N)^T$ とすれば $$ \begin{align} \textbf{$\omega$}_0^T \textbf{$\omega$}_0 & = \sum_{i = 1}^N \widetilde{\alpha}_i t_i {\bf x}_i^T \textbf{$\omega$}_0 = \sum_{i = 1}^N \widetilde{\alpha}_i (1 - t_i b_0) \\ & = \sum_{i = 1}^N \widetilde{\alpha}_i - b_0 \sum_{i = 0}^N \widetilde{\alpha}_i t_i = \sum_{i = 1}^N \widetilde{\alpha}_i \end{align} $$ なので、最大マージンは $$ D_{max} = \frac{1}{||\textbf{$\omega$}||} = \frac{1}{\sqrt{\textbf{$\omega$}_0^T \textbf{$\omega$}_0}} = \frac{1}{\sqrt{\sum_{i = 1}^N \widetilde{\alpha}_i }} $$
線形分離可能でない場合への拡張(1/7)
線形分離可能でない場合、制約条件を全て満たす解は求まらない
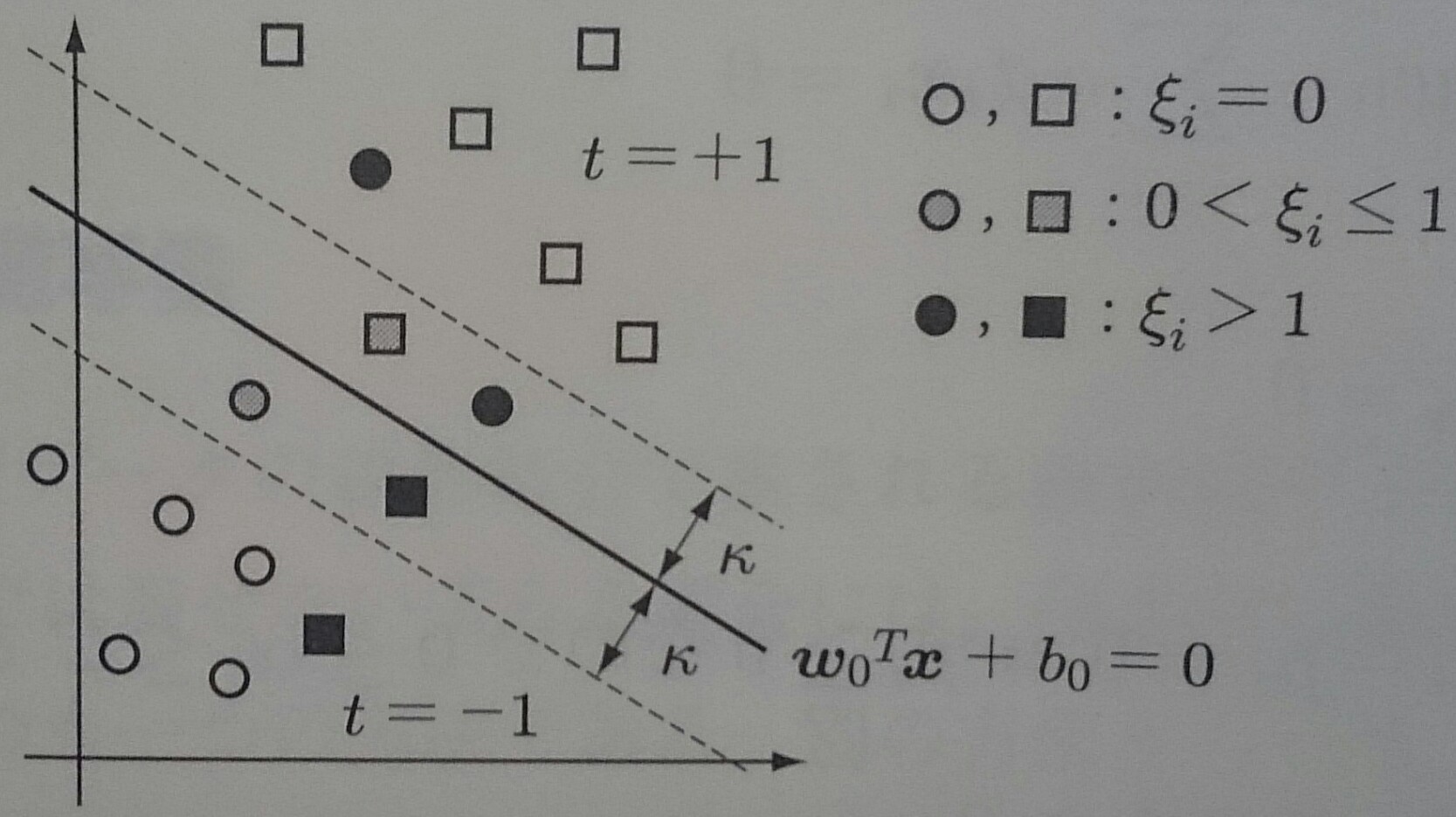
変数$\xi_i$を導入して $$ t_i(\textbf{$\omega$}^T {\bf x}_i + b) - 1 + \xi_i \geq 0 \\ \left\{ \begin{array}{ll} \xi_i = 0 & マージン内で識別可 \\ 0 < \xi_i \leq 1 & マージン境界外で識別可 \\ \xi_i > 1 & 誤識別 \end{array} \right.$$ とすれば、制約条件を満たすことができる
線形分離可能でない場合への拡張(2/7)
変数$\xi_i$をスラック変数といい、このような手法ををソフトマージン識別器という
全ての学習データのスラック変数の和$\sum_{i = 1}^N \xi_i \; (\xi_i \leq 0)$は 誤識別数の上限を与える
線形分離可能でない場合への拡張(3/7)
ソフトマージン識別器の主問題の定義は以下のようになる
評価関数 $$ L_p(\textbf{$\omega$}, \textbf{$\xi$}) = \frac{1}{2} \textbf{$\omega$}^T \textbf{$\omega$} + C \sum_{i = 1}^N \xi_i $$ 不等式制約条件 $$ t_i (\textbf{$\omega$}^T {\bf x}_i + b) - 1 + \xi_i \geq 0, \xi_i \geq 0 $$
パラメータ$C$は誤識別数に対するペナルティの強さを表し、大きいほど$\textbf{$\omega$}$ のノルム最小化よりも誤識別数を小さくする方を優先する解が得られる
線形分離可能でない場合への拡張(4/7)
ソフトマージン識別器の主問題に関するラグランジュ関数は $$ \begin{align} \widetilde{L}(\textbf{$\omega$}, b, \textbf{$\alpha$}, \textbf{$\xi$}, \textbf{$\mu$}) & = \frac{1}{2} \textbf{$\omega$}^T \textbf{$\omega$} + C \sum_{i = 1}^N \xi_i \\ & - \sum_{i = 1}^N \alpha_i (t_i (\textbf{$\omega$}^T {\bf x}_i + b) - 1 + \xi_i) - \sum_{i = 1}^N \mu_i \xi_i \end{align} $$
線形分離可能でない場合への拡張(5/7)
ソフトマージン識別器の主問題に対応するKKT条件は
- $\frac{\partial \widetilde{L}}{\partial \textbf{$\omega$}} |_{textbf{$\omega$} = \textbf{$\omega$}_0} = \textbf{$\omega$}_0 - \sum_{i = 1}^N \alpha_i t_i {\bf x}_i = 0 $
- $\frac{\partial \widetilde{L}}{\partial b} = \sum_{i = 1}^N \alpha_i t_i = 0$
- $\frac{\partial \widetilde{L}}{\partial b} = C - \alpha_i - \mu_i = 0 \Rightarrow \mu_i \geq 0 なので 0 \leq \alpha_i \leq C$
- $t_i(\textbf{$\omega$}^T {\bf x}_i + b) - 1 + \xi_i \geq 0$
- $\xi_i \geq 0, \alpha_i \geq 0, \mu_i \geq 0$
- $\alpha_i(t_i(\textbf{$\omega$}^T {\bf x}_i + b) - 1 + \xi_i) = 0$
- $\mu_i \xi_i = 0$
線形分離可能でない場合への拡張(6/7)
条件6,7が相補性条件
$\alpha_i < C$なら条件3より$\mu_i > 0$となるので、条件7が成り立つためには$\xi_i = 0$でなければならない
すなわち、${\bf x}_i$はマージン内で正しき識別できることになる
最適なバイアス$b_0$は$0 < \alpha_i < C$を満たすデータ点で計算する
線形分離可能でない場合への拡張(7/7)
ソフトマージン識別器の主問題に関するラグランジュ関数 に対する双対問題は線形分離可能な場合と同様にして得られ、以下のようになる
評価関数(最大化) $$ L_d(\textbf{$\alpha$}) = \textbf{$\alpha$}^T {\bf 1} - \frac{1}{2} \textbf{$\alpha$}^T {\bf H} \textbf{$\alpha$} $$ 制約条件 $$ 0 \leq \alpha_i \leq C, \;\; \textbf{$\alpha$}^T {\bf T} = 0 $$
非線形特徴写像(1/5)
SVMは、学習データの線型結合で表される識別超平面を構築する
識別境界が学習データの線形関数で表せない場合は、非線形識別関数を構築する方法もあるが、 非線形特徴写像を用いて非線形特徴空間に写像して、その空間内で線形識別関数を用いる方法がある
非線形特徴写像を用いる場合は試行錯誤で非線形特徴写像を決める必要がある
非線形特徴写像(2/5)
$d$次元の学習データ${\bf x} \in \cal{R}^d$と、その非線形写像の集合
$\{\varphi_j({\bf x})\}_{j=1}^M$を考える
非線形写像空間のベクトルを以下のように表し
$$ \textbf{$\varphi$}({\bf x}) = (\varphi_0({\bf x}) = 1, \varphi_1({\bf x}),
\ldots , \varphi_M({\bf x}))^T$$
非線形空間内でSVMを考えると、最適識別超平面は
$$ \textbf{$\omega$}_0 = \sum_{i = 1}^M \omega \varphi_j({\bf x})
= \textbf{$\omega$}^T \textbf{$\varphi$}({\bf x}) $$
となる
非線形特徴写像(3/5)
識別関数を以下のように $$ h(\textbf{$\varphi$}({\bf x})) = \textbf{$\omega$}_0^T \textbf{$\varphi$}({\bf x}) = \sum_{i = 1}^N \alpha_i t_i \textbf{$\varphi$}^T({\bf x}_i)\textbf{$\varphi$}({\bf x}) = \sum_{i = 1}^N \alpha_i t_i K({\bf x}_i, {\bf x}) $$ 元も空間のベクトルの関数$K({\bf x}_i, {\bf x})$を用いて表せれば都合がいい
このような関数$K({\bf x}_i, {\bf x})$をカーネル関数という
非線形特徴写像(4/5)
ソフトマージン識別器のラグランジュ未定乗数$\alpha_i$は次の双対問題を解くことで得られる
評価関数(最大化) $$ \begin{align} L_d(\textbf{$\alpha$}) & = \sum_{i = 1}^N \alpha_i - \frac{1}{2} \sum_{i = 1}^N \sum_{j = 1}^N \alpha_i \alpha_j t_i t_j \textbf{$\varphi$}^T({\bf x}_i \textbf{$\varphi$}({\bf x}_j) \\ & = \sum_{i = 1}^N \alpha_i - \frac{1}{2} \sum_{i = 1}^N \sum_{j = 1}^N \alpha_i \alpha_j t_i t_j K({\bf x}_i, {\bf x}) \end{align} $$ 制約条件 $$ 0 \leq \alpha_i \leq C, \;\; \textbf{$\alpha$}^T {\bf T} = 0 $$
非線形特徴写像(5/5)
$K({\bf x}_i, {\bf x}_j) = \varphi^T({\bf x}_i)\varphi({\bf x}_j)$を$(i, j)$要素とする $N \times N$対称行列${\bf K}({\bf X}, {\bf X})$をグラム行列という
${\bf X}=({\bf x}_1, \ldots , {\bf x}_N)^T$はデータ行列
非線形空間の次元が大きく$M \gg d$が成り立っている場合、非線形空間内で 線形分離可能になっても内積計算に時間がかかる
${\bf x}_i$と${\bf x}$の$d$次元空間内での内積計算で済ますことができる 高速なカーネル関数が存在し、内積カーネルと呼ばれる
多項式カーネル(1/3)
内積カーネルの1つ、$p$次の多項式カーネルはよく利用される $$ K_p({\bf u}, {\bf v}) = (\alpha + {\bf u}^T {\bf v})^p \;\;(\alpha \geq 0は実定数) $$
${\bf u} = (u_1, u_2)^T$、${\bf v} = (v_1, v_2)^T$、$\alpha = 1$、2次の多項式カーネルを $$ \begin{align} K_2({\bf u}, {\bf v}) & = (1 + {\bf u}^T {\bf v})^2 = (1 + u_1 v_1 + u_2 v_2)^2 \\ & = 1 + u_1^2 v_1^2 + 2 u_1 u_2 v_1 v_2 + u_2^2 v_2^2 + 2 u_1 v_1 + 2u_2 v_2 \end{align} $$ で定義する
多項式カーネル(2/3)
$K_2({\bf u}, {\bf v})$の${\bf u}$と${\bf v}$に由来した項を $$ \begin{align} \varphi({\bf u}) & = (1, u_1^2, \sqrt{2} u_1 u_2, u_2^2, \sqrt{2} u_1, \sqrt{2} u_2)^T \\ \varphi({\bf v}) & = (1, v_1^2, \sqrt{2} v_1 v_2, v_2^2, \sqrt{2} v_1, \sqrt{2} v_2)^T \end{align} $$ のように分離すれば、$K_2({\bf u}, {\bf v}) = \varphi({\bf u})^T \varphi({\bf v})$ と表現できたことになるので、6次元空間のベクトルの内積が2次元ベクトルの内積とスカラー値の2乗 で計算できることになる
多項式カーネル(3/3)
多項式カーネル$K_p({\bf u}, {\bf v})$による非線形特徴空間の次元$D(d, p)$は $$ D(d, p) = \left( \begin{array}{c} d + p \\ p \end{array} \right) $$ となる
$d=16\times16$画素からなる画像の$p=4$次の多項式カーネルの場合、非線形空間の次元は $186,043,585$となるが、学習データは一般的に極めて少ないので、高次元空間内にまばらに分布することになり、疎なカーネルマシンともよばれる
RBFカーネル
RBFカーネルは以下で定義される $$ K_{\sigma} ({\bf u}, {\bf v}) = \exp{(-\frac{1}{2\sigma^2} || {\bf u} - {\bf v}||^2)} $$
$\sigma$はカーネル関数の広がりを制御するパラメータで、$\sigma$が大きい場合は 入力データ${\bf x}$から遠く離れる広範囲のサポートベクトルが識別に寄与することになる