はじめてのパターン認識
7章
Created by 2GMon
話の流れ
- パーセプトロンの学習規則
- 誤差逆伝播法
パーセプトロン(1/3)
2クラスの線形識別関数を求める方法
2クラスの学習データが線形分離可能なら収束することが証明されている
パーセプトロンを多層化し非線形識別関数にすることで、線形分離可能性という条件を外した誤差逆伝播法もある
非線形なので局所解に陥ることがあり、人による解の解釈が難しいという欠点がある
パーセプトロン(2/3)
2クラス問題の線形識別関数 $f({\bf x}) = \textbf{$\omega$}^T {\bf x}$ は以下のようなネットワークモデルと見ることができる
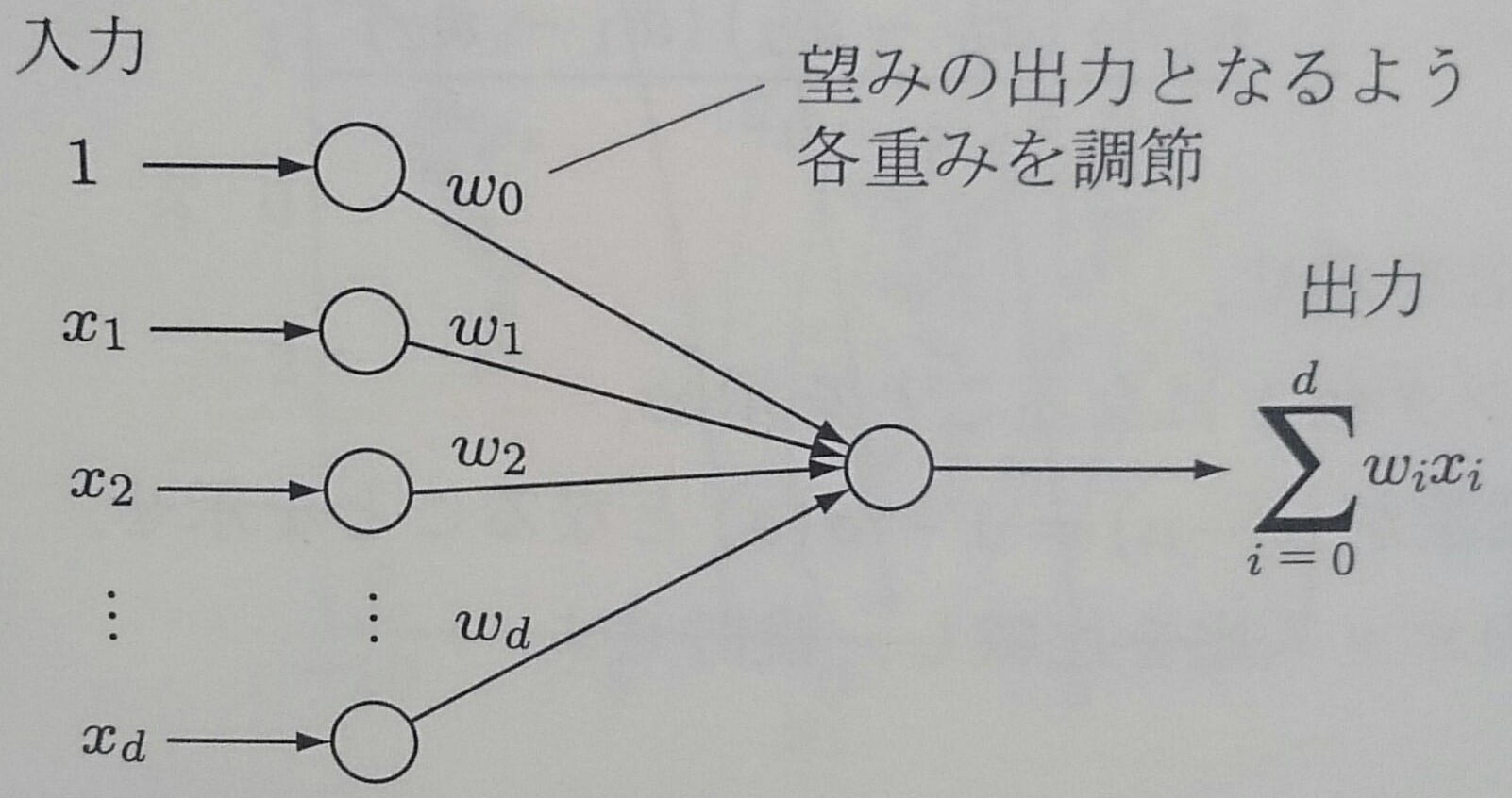
このようなネットワークモデルをパーセプトロンと呼ぶ
パーセプトロン(3/3)
データが線形分離可能なときに、$C_2$に属するデータの符号を反転させたものを考えると、全てのデータに対して、分類が正しければ $f({\bf x}) \geq 0$、 誤っていれば $f({\bf x}) < 0$ となる
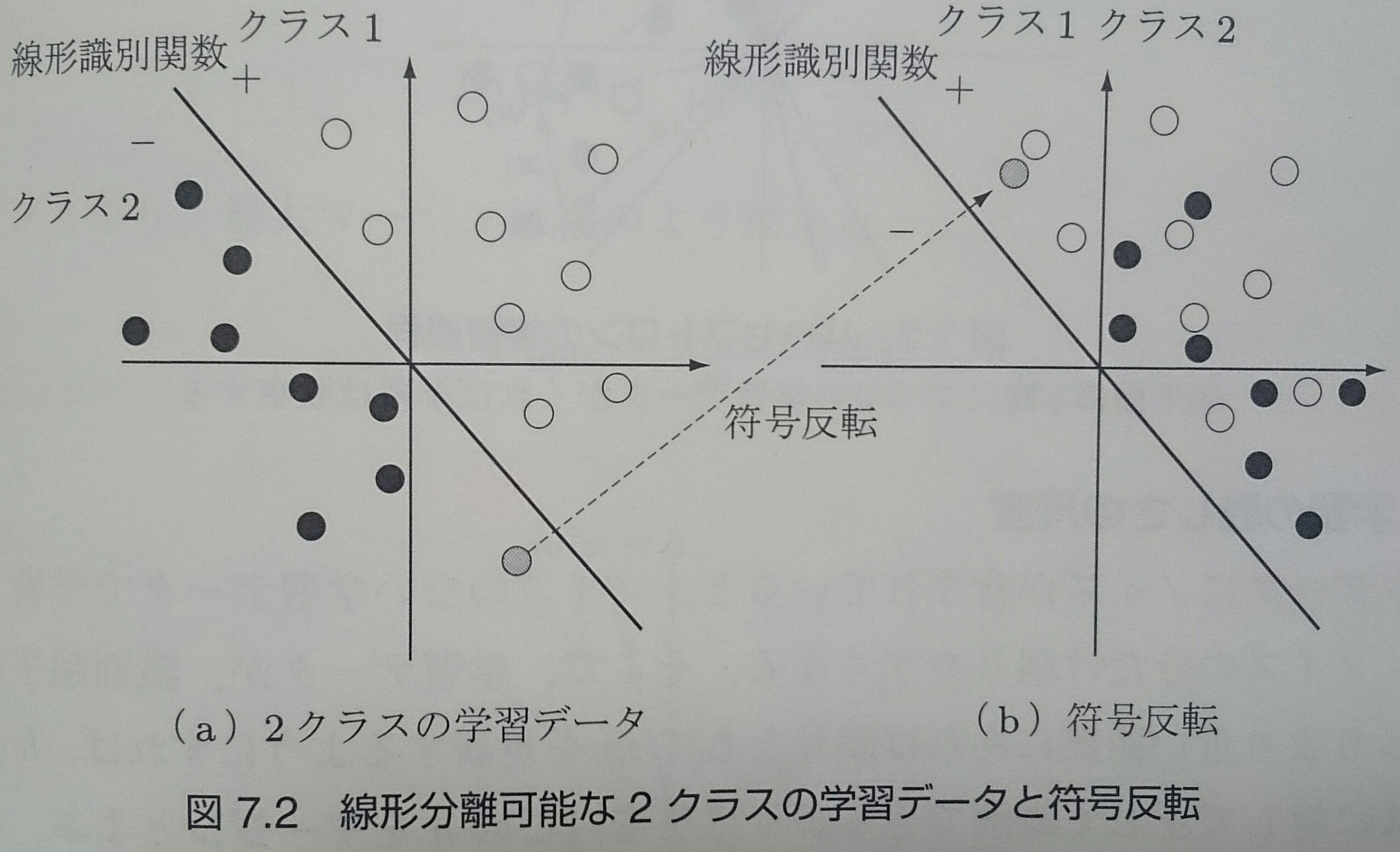
パーセプトロンの識別規則(1/2)
学習データの系列を ${\bf x}_1, {\bf x}_2, \ldots , {\bf x}_i , \ldots$ としたとき、パーセプトロンの学習規則は以下のようになる
$\eta$は収束速度を決めるパラメータで、$\eta = 1$ の場合を固定増分誤り訂正法とよぶ
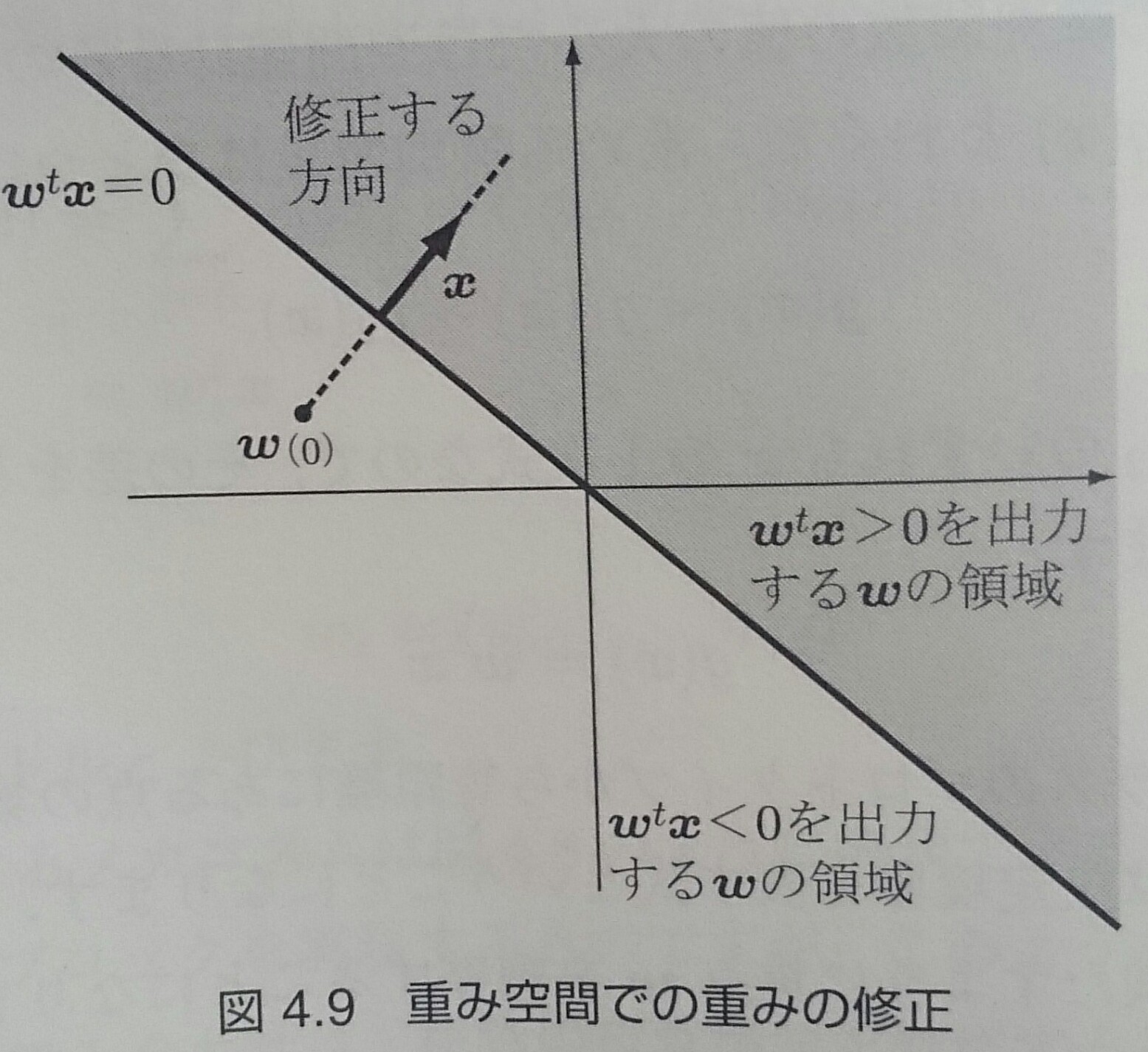
パーセプトロンの識別規則(2/2)
データ空間ではなく重み空間を考えると、 $\textbf{$\omega$}$ を ${\bf x}$ 方向に動かすのが一番効率よく重みを更新できることがわかる
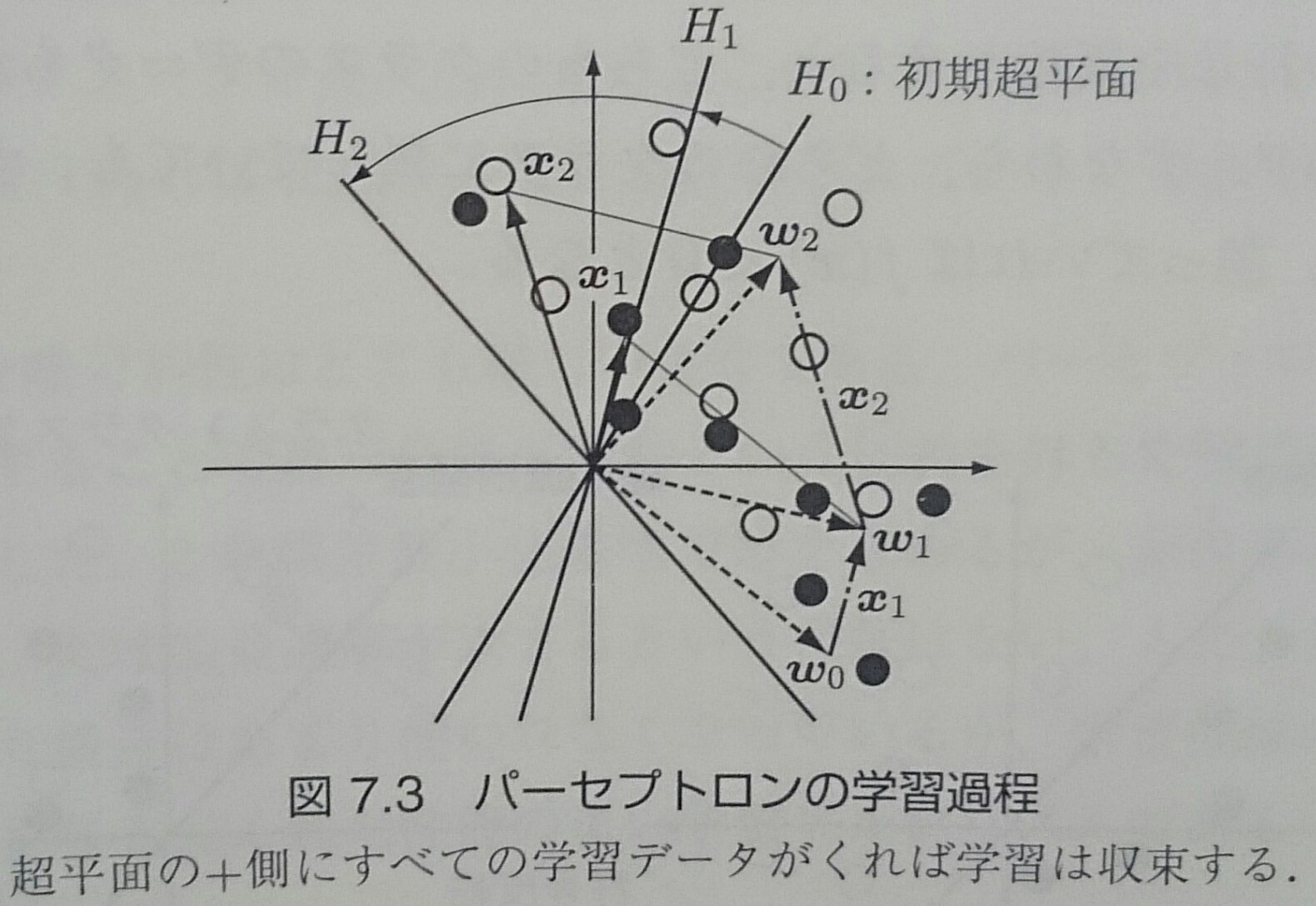
パーセプトロンの学習過程
マージン
テストデータにノイズが含まれていると、ノイズのない学習データで学習した識別関数はノイズの分だけ誤りが増える
そこで、学習データが識別超平面から距離$h > 0$ より近ければ誤りとして$\textbf{$\omega$}$を更新すれば、 $h$より小さいノイズに対して正しく識別できるようになる
$h$をマージンと呼ぶ
クラス間マージン$\rho$
ある識別関数$f({\bf x}) = \textbf{$\omega$}^T {\bf x} = 0$に対して取れるマージンの大きさ$D$は、 $C_1, C_2$の学習データを識別関数の法線ベクトル上に射影した長さの差の最小値の半分 $$ D = \frac{\rho}{2} = \frac{1}{2} ( \min_{{\bf x} \in C_1} \frac{\textbf{$\omega$}^T {\bf x}}{|| \textbf{$\omega$} ||} - \max_{{\bf x} \in C_2} \frac{\textbf{$\omega$}^T {\bf x}}{|| \textbf{$\omega$} ||}) $$
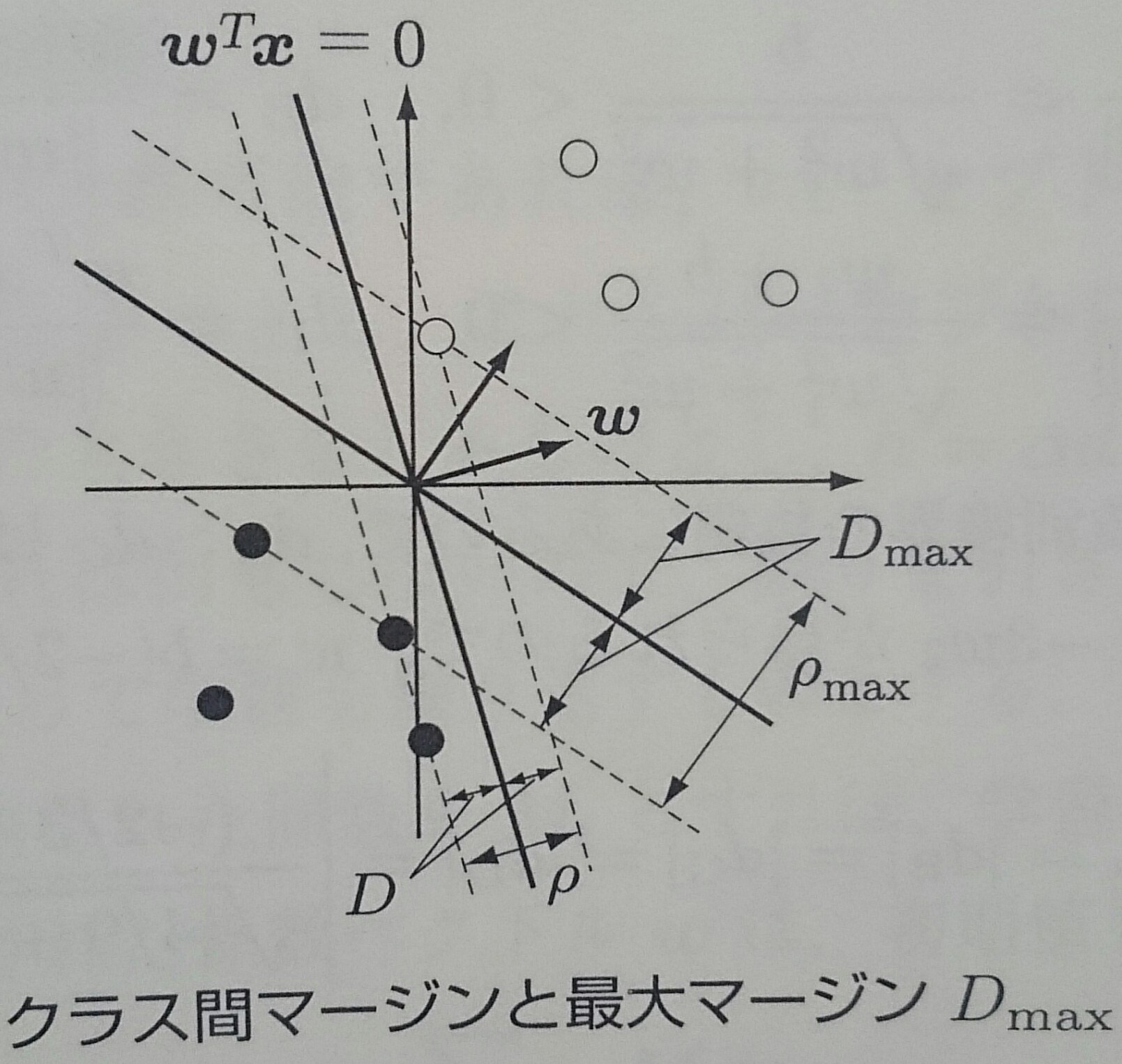
最大マージン$D_{max}$
最大マージン$D_{max}$は最大クラス間マージン$\rho_{max} = max_{\textbf{$\omega$}} \rho(\textbf{$\omega$})$を用いて表される $$ D_{max} = \frac{1}{2} \rho_{max} $$

与えられた学習データから互いのクラスに最も近い境界上の学習データを探しだし、$D_{max}$を満たす識別関数のパラメータを 求める手法がサポートベクトルマシン
パーセプトロンの収束定理
2クラスの学習データが線形分離可能なら、パーセプトロンの学習規則が有限回数の繰り返しで収束すること
誤りをおこす学習データのみの系列を考え、以下のようにする
- マージン$h$ : 次元ごとに$\alpha$の大きさをとるとして$h = \alpha d$
- 学習総数$M$ : $M = \sum_{i} M_i\;$ ($M_i$ : データ${\bf x}_i$が学習された回数)
- 係数ベクトル$\textbf{$\omega$}$ : 初期値を${\bf 0}$として $\textbf{$\omega$} = \eta \sum_{{\bf x}_i \in C_1, C_2}^{\;} M_i {\bf x}_i$
- 解ベクトル : $\textbf{$\omega$}^*$
パーセプトロンの収束定理(1/3)
解ベクトル$\textbf{$\omega$}^*$と$\textbf{$\omega$}$の内積は $$ \begin{align} \textbf{$\omega$}^T \textbf{$\omega$}^* & = \eta \sum_{{\bf x}_i \in C_1, C_2} M_i {\bf x}_i^T \textbf{$\omega$}^* \geq \eta M \min_{{\bf x}_i \in C_1, C_2} ({\bf x}_i^T \textbf{$\omega$}^*) \\ & = \eta M \min_{{\bf x}_i \in C_1, C_2} (\frac{{\bf x}_i^T \textbf{$\omega$}^*}{|| \textbf{$\omega$}^* ||} || \textbf{$\omega$}^* ||) = \eta M D(\textbf{$\omega$}^*) || \textbf{$\omega$}^* || \end{align} $$ となるので、学習中の係数ベクトルと解ベクトルの内積は$M$に比例して増加し、係数ベクトルは解ベクトルに近づいていく
パーセプトロンの収束定理(2/3)
各学習データの長さが$||{\bf x}_i||^2 \leq d$を満たしていると仮定し、${\bf x}_i$による係数ベクトルの変更量を求めると
$$ \begin{align} \Delta \textbf{$\omega$} & = || \textbf{$\omega$} + \eta {\bf x}_i ||^2 - || \textbf{$\omega$} ||^2
= \eta^2 ||{\bf x}||^2 + 2\eta \textbf{$\omega$}^T {\bf x}_i \\
& \leq \eta^2 d + 2\eta \alpha d = d \eta (\eta + 2\alpha) \end{align} $$
(係数ベクトルを更新するということは$\textbf{$\omega$}^T {\bf x}_i \leq h$が成り立っている)
となるので、$M$回学習した係数ベクトルの長さは$||\textbf{$\omega$}||^2 \leq Md\eta (\eta + 2\alpha)$ に抑えられる
パーセプトロンの収束定理(3/3)
$\textbf{$\omega$}$と$\textbf{$\omega$}^*$の方向余弦の2乗は $\theta = (\textbf{$\omega$}^T \textbf{$\omega$}^*)^2 / (||\textbf{$\omega$}||^2 ||\textbf{$\omega$}^*||^2) $ なので、 $$ M\frac{D^2(\textbf{$\omega$}^*) \eta}{d(\eta + 2\alpha)} \leq \theta \leq 1 \Rightarrow M \leq d \frac{1 + 2\alpha / \eta}{D_{max}^2} $$となり、学習回数に上限があるので学習は収束する
次元$d$とマージン$\alpha$が大きくなると学習回数が増え、2クラス間の距離が大きくなるほど$D_{max}^2$が大きくなるので 学習回数が少なくなる
多層パーセプトロン(1/6)
$x_1, x_2$の排他的論理和は線形識別関数で正しく識別できないが、第3の入力$x_3 = x_1 \times x_2$を作れば 3次元入力空間で線形分離可能になり、以下のような回路で実現できる
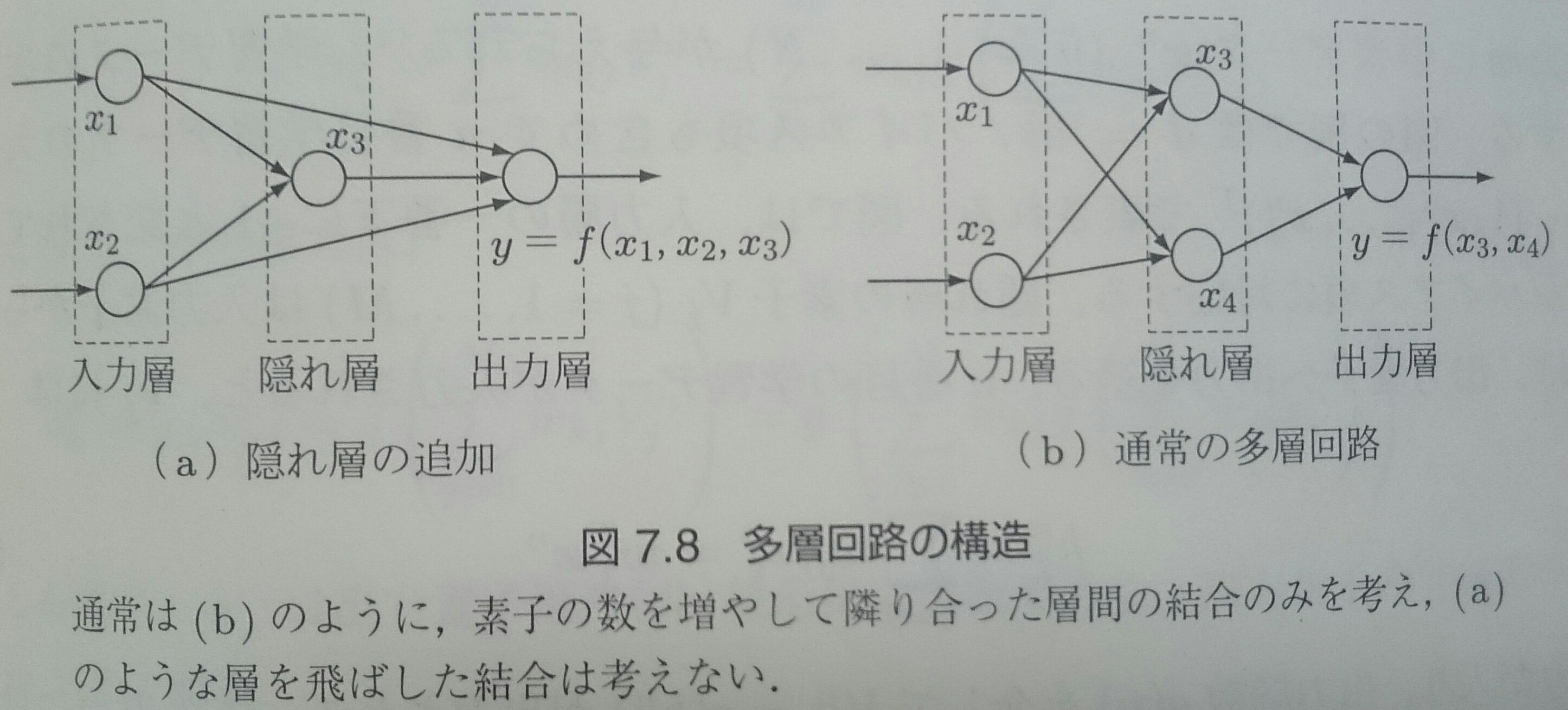
素子間の係数を学習するために多層パーセプトロンの誤差逆伝播法を用いる
多層パーセプトロン(2/6)
係数ベクトルと入力ベクトルの内積演算は以下のような2層からなる学習回路で表現できる (慣例的に入力層を数えない)
各層はそれぞれ、入力素子・隠れ素子・出力素子から成り立っている
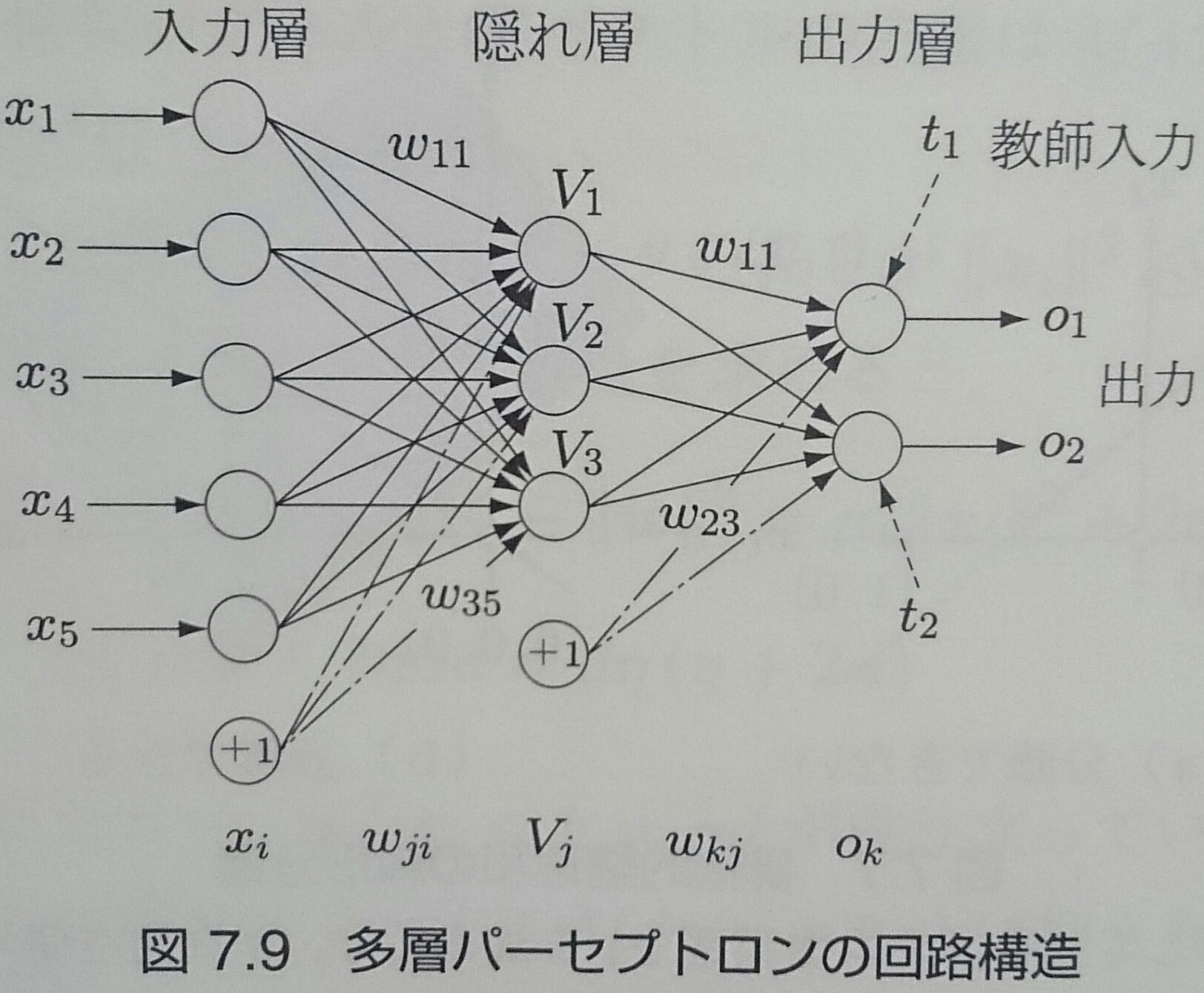
多層パーセプトロン(3/6)
$n$番目のデータが入力されると$V_j$に $h_j^n = \sum_{i = 0}^d \omega_{ji} x_i^n = \textbf{$\omega$}_j^T {\bf x}^n$ の入力が入り、出力関数$g(u)$ を介して $V_j^n = g(h_j^n)$ が出力される

隠れ素子の出力関数が線形なら、多層回路と等価な1層の回路が存在するので、$g(u)$は非線形でなければいけない
多層パーセプトロン(4/6)
$g(u)$は非線形出力関数と呼ばれるあらゆる$u$で微分可能な単調増加関数で、 シグモイド関数$g(u) = \frac{1}{1 + \exp(-\beta u)}$がよく使用される
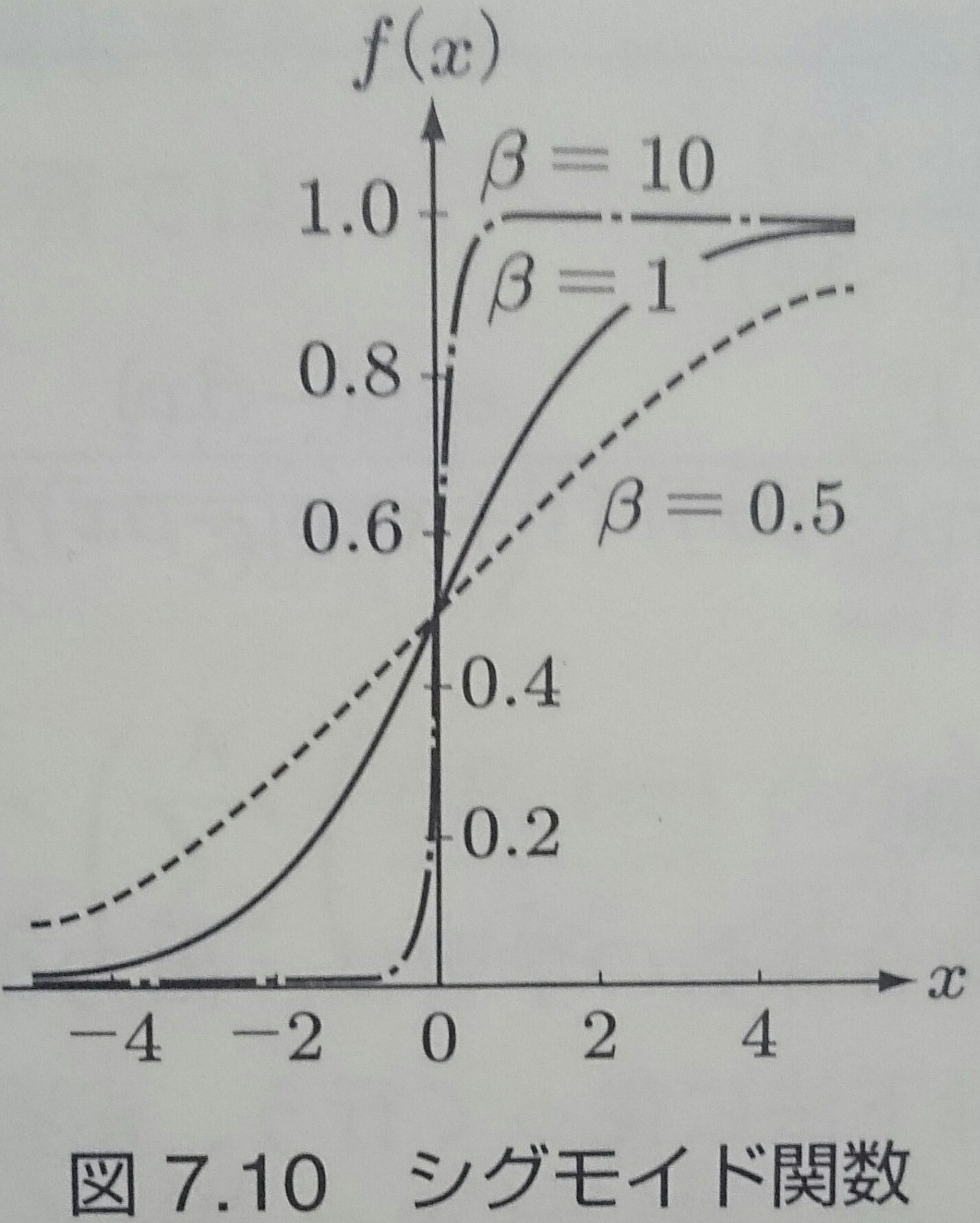
ロジスティック関数と同じ形だが、パラメータ$\beta$で関数の傾きが調整できるようになっていて、学習回路の分野では シグモイド関数と呼ばれる
多層パーセプトロン(5/6)
出力素子$o_k$への入力は $$ h_k^n = \sum_{j = 0}^M \omega_{kj} V_j^n = \sum_{j = 0}^M \omega_{kj} g(\sum_{i = 0}^d \omega_{ji} x_i^n) $$ で与えられ、出力は $$ o_k^n = \widetilde{g}(h_k^n) = \widetilde{g}(\sum_{j = 0}^M \omega_{kj} V_j^n) = \widetilde{g}(\sum_{j = 0}^M \omega_{kj} g(\sum_{i = 0}^d \omega_{ji} x_i^n)) $$で与えられる
$\widetilde{g}()$は出力素子用の(非)線形出力関数で、ソフトマックス関数 $\widetilde{g}(o_k^n) = \frac{\exp(o_k^n)}{\sum_{l = 1}^K \exp(o_l^n)}$ で確率的な解釈$\widetilde{g}(o_k^n) = p(t_k^n = 1| {\bf x}^n)$を与える場合もある
多層パーセプトロン(6/6)
誤差逆伝播法は非線形関数近似の問題にも使うことができ、この場合には出力関数は線形でいい
教師信号はアナログ値であり、この値を推定できるように最小2乗誤差基準で結合係数を学習する

誤差逆伝播法(1/5)
隠れ素子から出力素子への結合係数は、出力素子へ与えられる教師信号を用いて、最急降下法で2乗誤差最小化を行って学習する
$n$番目の学習データによる誤差の評価関数は $$ \begin{align} E_n(\textbf{$\omega$}) & = \frac{1}{2} \sum_{k = 1}^K (t_k^n - o_k^n)^2 = \frac{1}{2} \sum_{k = 1}^K (t_k^n - \widetilde{g}(h_k^n))^2 \\ & = \frac{1}{2} \sum_{k = 1}^K(t_k^n - \widetilde{g}(\sum_{j = 0}^M \omega_{kj} V_j^n))^2 \\ & = \frac{1}{2} \sum_{k = 1}^K(t_k^n - \widetilde{g}(\sum_{j = 0}^M \omega_{kj} g(\sum_{i = 0}^d \omega_{ji} x_i^n)))^2 \end{align}$$となるので、学習データ全体では$E(\textbf{$\omega$}) = \sum_{n = 1}^N E_n(\textbf{$\omega$})$
誤差逆伝播法(2/5)
学習データ全体を用いて結合係数の修正量を計算し更新することを1エポックといい、 $\tau$エポック目の修正量を$\Delta \omega_{kj}(\tau)$とすれば、 $\omega_{kj}(\tau + 1) = \omega_{kj}(\tau) + \Delta \omega_{kj}(\tau)$なので $$ \begin{align} \Delta \omega_{kj}(\tau) & = \sum_{n = 1}^N(- \eta \frac{\partial E_n(\textbf{$\omega$})}{\partial \omega_{kj}}) = - \eta \sum_{n = 1}^N (\frac{\partial E_n(\textbf{$\omega$})}{\partial o_k^n} \frac{\partial o_k^n}{\partial \omega_{kj}}) \\ & = \eta \sum_{n = 1}^N (t_k^n -o_k^n) \widetilde{g}'(h_k^n)V_j^n = \eta \sum_{n = 1}^N \delta_k^n V_j^n \end{align} $$
$\delta_k^n = (t_k^n - o_k^n)\widetilde{g}'(h_k^n)$は誤差信号という
出力関数$\widetilde{g}(h_k^n)$がシグモイド関数の場合、出力値が0と1に近い部分で0になり、学習が進まなくなることがある
誤差逆伝播法(3/5)
入力素子$x_i$から隠れ素子$V_j$への結合係数$\omega_{ji}$の学習のための評価関数は$\omega_{kj}$の場合と同様に $$ \begin{align} \Delta \omega_{ji}(\tau) & = \sum_{n = 1}^N (- \eta \frac{\partial E_n(\textbf{$\omega$})}{\partial \omega_{ji}}) = -\eta \sum_{n = 1}^N(\frac{\partial E_n(\textbf{$\omega$})}{\partial V_j^n} \frac{\partial V_j^n}{\partial \omega_{ji}}) \\ & = -\eta \sum_{n = 1}^N(\sum_{k = 1}^K(\frac{\partial E_n(\textbf{$\omega$})}{\partial o_k^n} \frac{\partial o_k^n}{\partial V_j^n}) \frac{\partial V_j^n}{\partial \omega_{ji}}) \\ & = \eta \sum_{n = 1}^N \sum_{k = 1}^K (t_k^n - o_k^n) \widetilde{g}'(h_k^n) \omega_{kj} g'(h_j^n) x_i^n \\ & = \eta \sum_{n = 1}^N \sum_{k = 1}^K \delta_k^n \omega_{kj} g'(h_j^n) x_i^n \end{align} $$
誤差逆伝播法(4/5)
隠れ素子$j$の誤差信号を $$\delta_j^n = g'(h_j^n) \sum_{k = 1}^N \delta_k^n \omega_{kj}$$ で定義すれば、 $$ \begin{align} \Delta \omega_{ji}(\tau) & = \eta \sum_{n = 1}^N \sum_{k = 1}^K \delta_k^n \omega_{kj} g'(h_j^n) x_i^n \\ & = \eta \sum_{n = 1}^N \delta_j^n x_i^n \end{align}$$ と表現できる
$\sum_{k = 1}^K \delta_k^n \omega_{kj}$の項は、核出力素子で発生した誤差$\delta_k^n$を、結合係数$\omega_{kj}$を介して 出力素子$k (= 1, \ldots , K)$から隠れ素子$j$へ戻しているので誤差逆伝播法と呼ばれる
誤差逆伝播法(5/5)
$n$番目の学習データによる$\omega_{kj}, \; \omega_{ji}$の修正量を以下のような式で与える場合は確率降下法という $$ \Delta \omega_{kj}^n(\tau) = \eta \delta_k^n(\tau)V_j^n(\tau) \\ \Delta \omega_{ji}^n(\tau) = \eta \delta_j^n(\tau) x_i^n(\tau) $$
誤差逆伝播法の学習特性
誤差逆伝播法は最急降下法や共役勾配法で解くことが多く、局所最適解に陥ることが多い
また、結果が結合係数の初期値に依存する
隠れ素子の数が増えると過学習が生じるので、交差検定などで最適な隠れ素子の数を決める必要がある
正則化(1/3)
結合係数が大きくなって、シグモイド関数の線形動作の領域から非線形動作の領域に入った時に ノイズ成分に適合して過学習が生じやすい
以前は、学習を進めながら汎化誤差を推定し、汎化誤差が上昇し始める手前で学習を終わらせる早期終了規則が用いられていた
最近では、学習が進んでも結合係数の大きさを抑えることができる正則化がよく用いられる
正則化(2/3)
正則化は誤差の評価関数$E(\textbf{$\omega$}) = \sum_{n = 1}^N E_n(\textbf{$\omega$})$にペナルティ項を加えて実現される $$ \begin{align} \widetilde{E}(\textbf{$\omega$}) & = E(\textbf{$\omega$}) + \lambda R(\textbf{$\omega$}) \\ & = \frac{1}{2} \sum_{n = 1}^N \sum_{k = 1}^K (t_k^n - o_k^n)^2 + \lambda (\sum_{i = 0}^d \sum_{j = 1}^M \omega_{ji}^2 + \sum_{j = 0}^M \sum_{k = 1}^K \omega_{kj}^2) \end{align} $$ この正則化を荷重減衰ペナルティという
正則化(3/3)
学習規則 $$ \begin{align} \Delta \omega_{kj}(\tau) & = \sum_{n = 1}^N(- \eta \frac{\partial E_n(\textbf{$\omega$})}{\partial \omega_{kj}}) = - \eta \sum_{n = 1}^N (\frac{\partial E_n(\textbf{$\omega$})}{\partial o_k^n} \frac{\partial o_k^n}{\partial \omega_{kj}}) \\ & = \eta \sum_{n = 1}^N (t_k^n -o_k^n) \widetilde{g}'(h_k^n)V_j^n = \eta \sum_{n = 1}^N \delta_k^n V_j^n \end{align} $$ に正則化項を加えて $$ \Delta \omega_{kj}(\tau) = \sum_{n = 1}^N(-\eta \frac{\partial E_n(\textbf{$\omega$}) + \lambda R(\textbf{$\omega$})}{\partial \omega_{kj}}) = \eta \sum_{n = 1}^N \delta_k^n V_j^n - 2\lambda \omega_{kj} $$ のように変更すれば$\omega_{kj}$が変更量に負帰還をかける形になるので、結合係数が大きくなるのを抑えられる
隠れ層の数と識別能力
誤差逆伝播法は隠れ層がいくつあっても出力層の誤差を伝播できるが、隠れ素子が非線形出力関数で構成されるので、 局所最適解が多くなり、大域的な最適化がさらに難しくなる
しかし、隠れ層が増えると、以下のように表現力が増える
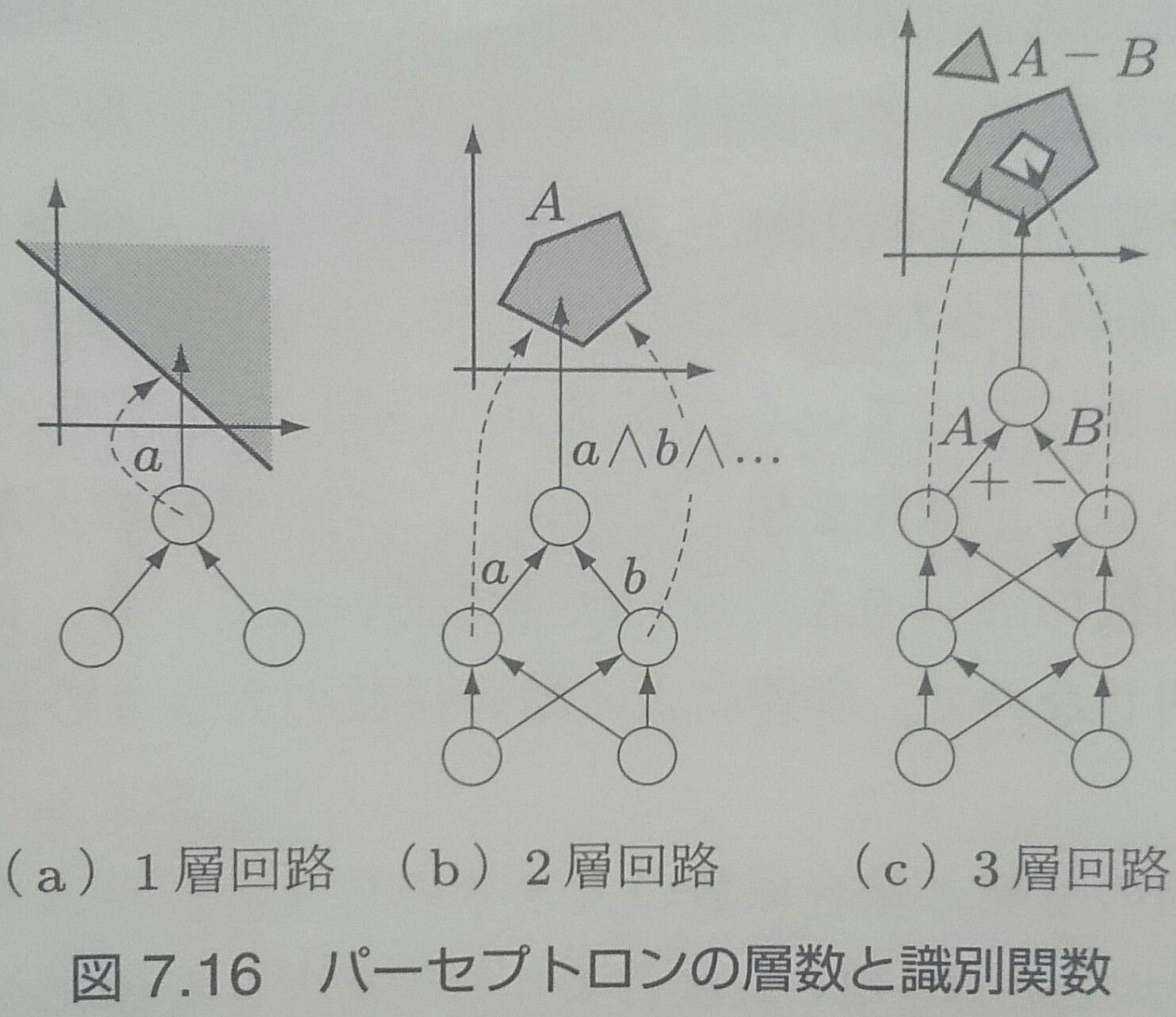
1層:直線のみ
2層:直線を組み合わせた凸領域
3層:凸領域を組み合わせた穴や飛び地
学習回路の尤度(1/3)
誤差逆伝播法の評価関数は $$ E_n(\textbf{$\omega$}) = \frac{1}{2} \sum_{k = 1}^K (t_k^n -o_k^n)^2 = \frac{1}{2} \sum_{k = 1}^K(t_k^n - \widetilde{g}(\sum_{j = 0}^M \omega_{kj} g(\sum_{i = 0}^d \omega_{ji} x_i^n)))^2 $$ が最もよく使われるが、ソフトマックス関数$\widetilde{g}(o_k^n) = \frac{\exp(o_k^n)}{\sum_{l = 1}^K \exp(o_l^n)}$で 出力を$\widetilde{g}(o_k) = p(t_k = 1 | {\bf x})$のようにする場合、全体を1に正規化しているので、 1-of-K符号化による確率として解釈でき、評価関数は $$ E(\textbf{$\omega$}) = - \sum_{n = 1}^N \sum_{k = 1}^K t_k^n \log o_k^n $$ で与えられる
この場合はロジスティック回帰と同様の表現になり、最尤推定法で更新式を得られる
学習回路の尤度(2/3)
出力$o_k$を$K$個の無関係な確率とみなす場合は、ベルヌーイ試行 $p({\bf t}|{\bf x}, \textbf{$\omega$}) = \prod_{k = 1}^K o_k^{t_k}(1 - o_k)^{1 - t_k}$ と解釈できるので、 負の対数尤度は、交差エントロピー型誤差関数 $$ E(\textbf{$\omega$}) = - \sum_{n = 1}^N \sum_{k = 1}^K (t_k^n \ln o_k^n + (1 - t_k^n) \ln (1 - o_k^n)) $$ となり、出力素子の学習は $$ \Delta \omega_{kj} = - \eta \frac{\partial E(\textbf{$\omega$})}{\partial \omega_{kj}} = \eta \sum_{n = 1}^N \frac{t_k^n - o_k^n}{o_k^n (1 - o_k^n)} g'(\sum_{j = 0}^M \omega_{kj} V_j^n) V_j^n $$ となる
学習回路の尤度(3/3)
出力関数がシグモイド関数の場合は $$ g'(\sum_{j = 0}^M \omega_{kj} V_j^n) = \beta o_k^n(1 - o_k^n) $$ なので、 $$ \Delta \omega_{kj} = \eta \sum_{n = 1}^N \delta_k^n V_j^n,\;\;\;\delta_k^n = \beta(t_k^n - o_k^n) $$ となり、出力関数の微分が消えるので、2乗誤差基準と違って非線形部分で学習が進まなくなることがない