はじめてのパターン認識
6章
Created by 2GMon
話の流れ
- 線形識別関数の定義
- パラメータの決定方法
線形識別関数
4章で正規分布から線形識別関数を導いたように、線形識別関数は一般に $$ f({\bf x}) = \textbf{$\omega$}^T {\bf x} + \omega_0 $$ という形で表される
線形識別関数の識別境界は、入力データが$d$次元の時、$d-1$次元の超平面になる
識別境界では$\textbf{$\omega$}^T {\bf x} = - \omega_0$が成り立つ
多クラス問題の線形識別関数の作り方は複数存在する
- 一対他(one versus the rest)
- 一対一(one versus one)
- 最大識別関数法
一対他
$f_j({\bf x})\;(j = 1, \ldots , K - 1)$
クラス$j$とそれ以外の全てのクラスを識別する線形識別関数
- 複数の識別関数が$>0$となる場合に識別できない
- 正のクラスのデータ数が負のクラスのデータ数に比べて少なくなりすぎる
一対一
クラス$i$と$j$を識別する$K(K - 1)/2$個の2クラス識別関数 $f_{ij} ({\bf x}) \; (1 \leq i < j \leq K)$ を用意し、 識別関数の多数決でクラスを決定する
- 識別関数同士で矛盾が生じる領域の識別ができない
- 入力データのクラスの直接関係ない識別関数がたくさんあるので、正確に多数決をとれない
最大識別関数法
クラス$i$と$j$の識別境界は$f_i({\bf x}) = f_j({\bf x})$なので $$ f_{ij} ({\bf x}) = (\textbf{$\omega$}_i - \textbf{$\omega$}_j)^T {\bf x} + (\omega_{i0} - \omega_{j0}) = 0 $$ を満たす$K-1$個の識別境界ができる
- 識別境界上以外の点は必ず識別できる
- 各クラスの占める領域は単連結で凸になる
単連結
穴の開いていない領域のこと
凸
領域内の任意の2点を結ぶ直線上のすべての点が、その領域に含まれている
あるクラス$i$の領域に属する点${\bf x}_1, {\bf x}_2$を結ぶ直線上の点${\bf x}^*$を考える
${\bf x}^*$は$0 \leq \lambda \leq 1$に対して $$ {\bf x}^* = \lambda {\bf x}_1 + (1 - \lambda) {\bf x}_2 $$ と表されるので、識別関数の線形性より $$ f_i({\bf x}^*) = \lambda f_i ({\bf x}_1) + (1 - \lambda) f_i ({\bf x}_2) $$ が成り立つ
クラス$i$の領域内では $f_i ({\bf x}_1) > f_{j \neq i}({\bf x}_1)$ と $f_i ({\bf x}_2) > f_{j \neq i}({\bf x}_2)$ が成り立っているので $f_i ({\bf x}^*) > f_{j \neq i}({\bf x}^*)$ が成り立つ
パラメータの推定
- 最小2乗誤差基準
- フィッシャーの判別関数
- ロジスティック回帰
最小2乗誤差基準
識別関数の出力値と教師入力との差を最小にするパラメータを求める手法で、解析的に解ける
係数ベクトル$\textbf{$\omega$} = (\omega_0, \omega_1, \ldots , \omega_d)^T$、$i$番目の学習データ ${\bf x}_i = (x_{i0}, x_{i1}, \ldots , x_{id})\;(x_{i0} = 1)$ と定義すると、識別関数は $$ f({\bf x}) = \omega_0 + \omega_1 x_1 + \cdots + \omega_d x_d = \textbf{$\omega$}^T {\bf x} $$ と表される
データ${\bf x}_i$が所属するクラスは、以下のように与えられる $$ t_i = \left\{ \begin{array}{l} 1\;({\bf x}_i \in C_1) \\ -1\;({\bf x}_i \in C_2) \end{array} \right. $$
学習データ数を$N$とし、行列${\bf X}$,ベクトル${\bf t}$を以下のように定義する $$ {\bf X} = ({\bf x}_1 , \cdots , {\bf x}_N)^T, \;\; {\bf t} = (t_1, \cdots , t_N)^T $$
評価関数$E(\textbf{$\omega$})$は識別関数の出力値と教師信号の差の2乗誤差 $$ E(\textbf{$\omega$}) = \sum_{i=1}^N (t_i - f({\bf x}_i))^2 = ({\bf t} - {\bf X} \textbf{$\omega$})^T ({\bf t} - {\bf X} \textbf{$\omega$}) $$
$E(\textbf{$\omega$})$を最小にするパラメータ$\textbf{$\omega$}$は$E(\textbf{$\omega$})$を$\textbf{$\omega$}$で 微分して0と置くことで得られるので $$ \begin{align} \frac{\partial E(\textbf{$\omega$})}{\partial \textbf{$\omega$}} & = \frac{{\bf t}^T{\bf t} - \textbf{$\omega$}^T {\bf X}^T {\bf t} - {\bf t}^T {\bf X} \textbf{$\omega$} + \textbf{$\omega$}^T {\bf X}^T {\bf X} \textbf{$\omega$}}{\partial \textbf{$\omega$}} \\ & = \frac{{\bf t}^T{\bf t} - {\bf t}^T {\bf X} \textbf{$\omega$} - {\bf t}^T {\bf X} \textbf{$\omega$} + \textbf{$\omega$}^T {\bf X}^T {\bf X} \textbf{$\omega$}}{\partial \textbf{$\omega$}} \\ & = \frac{{\bf t}^T{\bf t} - 2 {\bf X}^T {\bf t} \textbf{$\omega$} + \textbf{$\omega$}^T {\bf X}^T {\bf X} \textbf{$\omega$}}{\partial \textbf{$\omega$}} \\ & = -2{\bf X}^T{\bf t} + ({\bf X}^T{\bf X} + {\bf X}{\bf X}^T)\textbf{$\omega$} \\ & = -2{\bf X}^T({\bf t} - {\bf X} \textbf{$\omega$}) = 0 \end{align}$$ よって$ \hat{\textbf{$\omega$}} = ({\bf X}^T {\bf X})^{-1} {\bf X}^T {\bf t} $
$ \hat{\textbf{$\omega$}} = ({\bf X}^T {\bf X})^{-1} {\bf X}^T {\bf t} $を正規方程式といい、 学習データに対する予測値 $\hat{{\bf t}}$は以下の式で得られる $$ \hat{{\bf t}} = {\bf X} \hat{\textbf{$\omega$}} = {\bf X} ({\bf X}^T {\bf X})^{-1} {\bf X}^T {\bf t} $$
行列 $ {\bf X} ({\bf X}^T {\bf X})^{-1} {\bf X}^T $ は教師データ $ {\bf t} $ を予測値 $ \hat{{\bf t}} $ に変換する行列で ハット行列と呼ばれる
多クラス問題へ拡張するためには$K$個の識別関数 $ f_k({\bf x}) = \textbf{$\omega$}_k^T {\bf x} $ を用意して、パラメータ$\textbf{$\omega$}_k $を2クラスと同様に求めればいい
2クラス問題と違って、一つの学習データにクラス数と同じ$K$個の教師入力が必要になり、$i$番目の教師入力は $ {\bf t}_i = (t_{i1}, \ldots , t_{iK}) $のダミー変数で与えられる
$N$個の学習データ $ {\bf X} = ({\bf x}_1, \ldots , {\bf x}_N)^T $ に対する教師データを $ {\bf T} = ({\bf t}_1, \ldots , {\bf t}_N)^T $とすると、2乗誤差を最小にするパラメータは $$ \hat{{\bf W}} = ({\bf X}^T {\bf X})^{-1} {\bf X}^T {\bf T} $$ で与えられる
最適なパラメータが求まったとき、識別関数は $$ G({\bf x}) = \hat{{\bf W}}^T {\bf x} = (\textbf{$\omega$}_1, \cdots , \textbf{$\omega$}_K)^T {\bf x} = (g_1({\bf x}), \cdots , g_K({\bf x}))^T $$ となり、識別規則は以下のようになる $$ 識別クラス = argmax_j \; g_j({\bf x}) $$
ただし、最大識別法では、複数のクラスが一直線上に並んでいるような分布の場合うまく識別できない
線形判別分析
線形識別関数は、$d$次元ベクトルを${\bf x}$を、ベクトル$\textbf{$\omega$}$上のスカラー関数$f({\bf x})$に写像していると考えることができる
線形判別分析はクラス間の分布ができるだけ重ならないような写像方向を見つける
線形判別分析の目的はクラス分離を良くすることで、クラスを識別する機能は無い
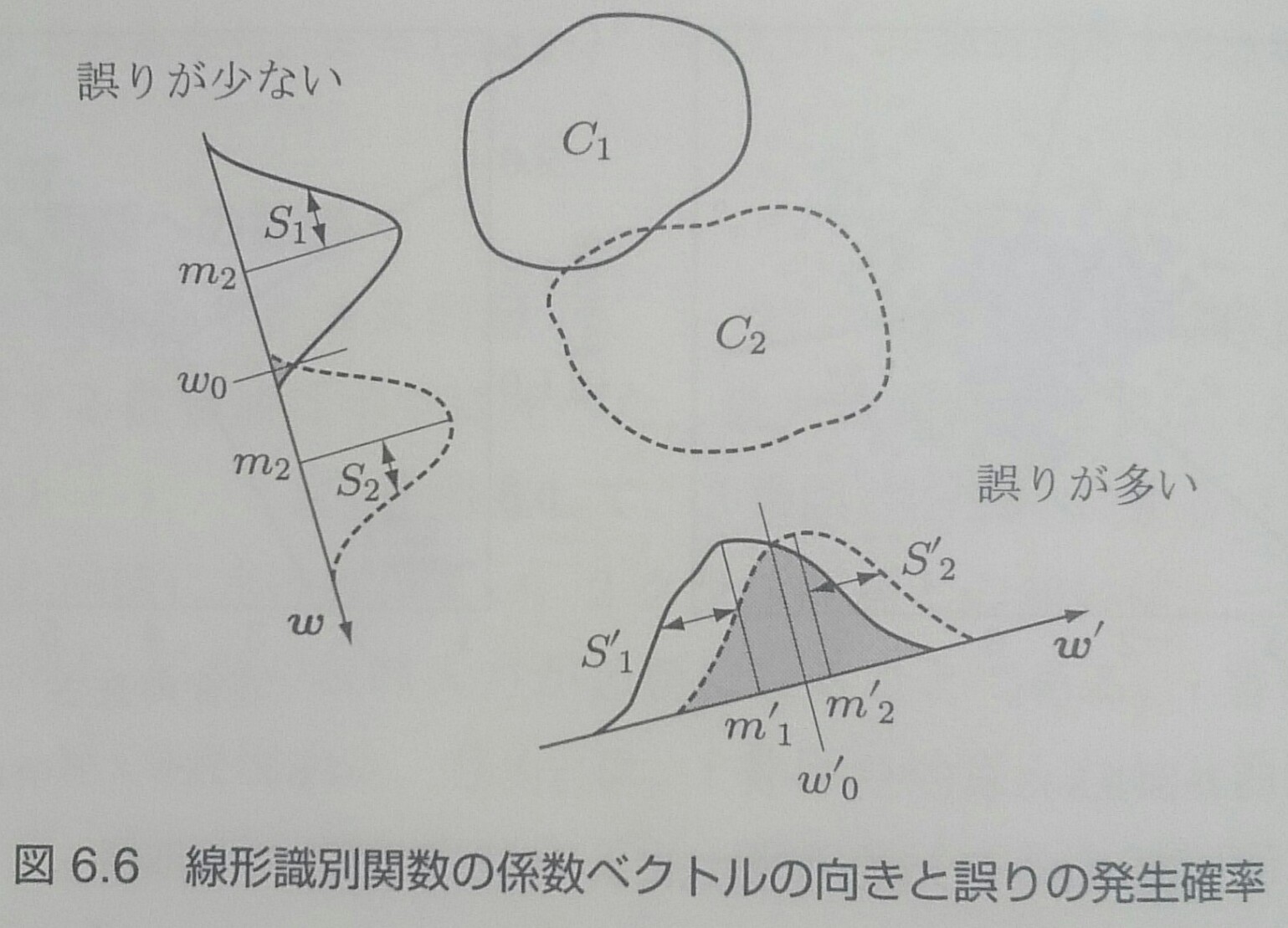
重なりの少ない写像を実現するベクトル$\textbf{$\omega$}$を見つけることが必要になる
フィッシャーの線形判別関数
クラス$(C_1, C_2)$、各クラスの学習データ数$N_1, N_2$のとき、線形識別関数$y=\textbf{$\omega$}^T{\bf x}$は線形変換なので、 平均ベクトル$m_k$を $m_k=\textbf{$\omega$}^T \textbf{$\mu$}_k$に写像する
各クラスの平均値の差が大きいほどクラスの分離がよく、クラスごとのデータの分布の広がりが小さいほうが、クラス間の重なりが小さくなることが期待できる
クラス間変動
平均値の差$m_1 - m_2 = \textbf{$\omega$}^T (\textbf{$\mu$}_1 - \textbf{$\mu$}_2)$の2乗
クラス内変動
$S_k^2 = \sum_{i \in C_k} (y_i - m_k)^2$
全クラス内変動は$S_1^2 + S_2^2$になる
フィッシャーの基準
クラス間変動とクラス内変動の比 $$ J(\textbf{$\omega$}) = \frac{(m_1 - m_2)^2}{S_1^2 + S_2^2} $$
フィッシャーの基準を最大にする$\textbf{$\omega$}$がクラスを最もよく分離する写像になる
クラス内変動は以下のように表現できる $$ \begin{align} (m_1 - m_2)^2 & = (\textbf{$\omega$}^T (\textbf{$\mu$}_1 - \textbf{$\mu$}_2))^2 \\ & = (\textbf{$\omega$}^T(\textbf{$\mu$}_1 - \textbf{$\mu$}_2)) (\textbf{$\omega$}^T(\textbf{$\mu$}_1 - \textbf{$\mu$}_2))^T \\ & = \textbf{$\omega$}^T (\textbf{$\mu$}_1 - \textbf{$\mu$}_2) (\textbf{$\mu$}_1 - \textbf{$\mu$}_2)^T \textbf{$\omega$} \\ & = \textbf{$\omega$}^T {\bf S}_B \textbf{$\omega$} \end{align} $$
クラス内変動も同様に以下のように表現できる $$ \begin{align} S_k^2 & = \sum_{i \in C_k} (y_i - m_k)^2 = \sum_{i \in C_k} (\textbf{$\omega$}^T ({\bf x}_i - \textbf{$\mu$}_k))^2 \\ & = \sum_{i \in C_k} (\textbf{$\omega$} ({\bf x}_i - \textbf{$\mu$}_k)) (\textbf{$\omega$} ({\bf x}_i - \textbf{$\mu$}_k))^T \\ & = \textbf{$\omega$} \left( \sum_{i \in C_k} ({\bf x}_i - \textbf{$\mu$}_k) ({\bf x}_i - \textbf{$\mu$}_k)^T \right) \textbf{$\omega$} \\ & = \textbf{$\omega$}^T {\bf S}_k \textbf{$\omega$} \end{align} $$
全クラス内変動は以下のようになるので $$ S_1^2 + S_2^2 = \textbf{$\omega$}^T ({\bf S}_1 + {\bf S}_2) \textbf{$\omega$} = \textbf{$\omega$}^T {\bf S}_W \textbf{$\omega$} $$ フィッシャーの基準は $$ J(\textbf{$\omega$}) = \frac{\textbf{$\omega$}^T {\bf S}_B \textbf{$\omega$}}{\textbf{$\omega$}^T {\bf S}_W \textbf{$\omega$}} $$となる
この式を最大化する解は、次の一般化固有問題を解くことで得られる $$ {\bf S}_B \textbf{$\omega$} = \lambda {\bf S}_w \textbf{$\omega$} $$ しかし、${\bf S}_w$が正則行列なら${\bf S}_w^{-1} {\bf S}_B \textbf{$\omega$} = \lambda \textbf{$\omega$}$ と書けるので、 通常の固有値問題となる
${\bf S}_B \textbf{$\omega$} = (\textbf{$\mu$}_1 - \textbf{$\mu$}_2) (\textbf{$\mu$}_1 - \textbf{$\mu$}_2)^T \textbf{$\omega$} \propto (\textbf{$\mu$}_1 - \textbf{$\mu$}_2)$なので、 $$ \textbf{$\omega$} \propto {\bf S}_W^{-1} {\bf S}_B \textbf{$\omega$} \propto {\bf S}_w^{-1}(\textbf{$\mu$}_1 - \textbf{$\mu$}_2) $$がフィッシャーの基準による最適な$\textbf{$\omega$}$となる
$\omega_0$は識別境界を与えるバイアス項だが、フィッシャーの基準では $m_1 - m_2$の項で$\omega_0$が消去されてしまうため、 直接求められない
クラス条件付き確率$p({\bf x}|C)\;(k=1,2)$が同じ共分散行列 $$ \textbf{$\Sigma$}_{pool} = P(C_1) \textbf{$\Sigma$}_1 + P(C_2) \textbf{$\Sigma$}_2 $$ を持つ多次元正規分布関数と仮定できれば $$ \textbf{$\Sigma$}_{pool} = \frac{1}{N} {\bf S}_W $$ となり、共分散行列と全クラスのクラス内変動行列は比例定数の違いのみになる
正規分布を線形写像しても正規分布なので、$\textbf{$\omega$}$上に写像されたデータのクラス条件付き分布を1次元正規分布関数で近似し、事後確率が同じになる点を$\omega_0$とすればいい
判別分析法
線形変換後の$y = \textbf{$\omega$}^T {\bf x}$の平均と分散は、クラス$k = 1, 2$について $$ m_k = \textbf{$\omega$}^T \textbf{$\mu$}_k + \omega_0 \\ \sigma_k^2 = \textbf{$\omega$}^T \textbf{$\Sigma$}_k \textbf{$\omega$} $$で定義される
クラス分離度の評価関数を$h(m_1, \sigma_1^2, m_2, \sigma_2^2)$で表すと、これを最大にする$\textbf{$\omega$}$と$\omega_0$は、 $h$をそれらで微分して0と置くと求まるので $$ \frac{\partial h}{\partial \textbf{$\omega$}} = \frac{\partial h}{\partial \sigma_1^2} \frac{\partial \sigma_1^2}{\partial \textbf{$\omega$}} + \frac{\partial h}{\partial \sigma_2^2} \frac{\partial \sigma_2^2}{\partial \textbf{$\omega$}} + \frac{\partial h}{\partial m_1} \frac{\partial m_1}{\partial \textbf{$\omega$}} + \frac{\partial h}{\partial m_2} \frac{\partial m_2}{\partial \textbf{$\omega$}} = 0 \\ \frac{\partial h}{\partial \omega_0} = \frac{\partial h}{\partial \sigma_1^2} \frac{\partial \sigma_1^2}{\partial \omega_0} + \frac{\partial h}{\partial \sigma_2^2} \frac{\partial \sigma_2^2}{\partial \omega_0} + \frac{\partial h}{\partial m_1} \frac{\partial m_1}{\partial \omega_0} + \frac{\partial h}{\partial m_2} \frac{\partial m_2}{\partial \omega_0} = 0 $$ を解けばいい
$$ \frac{\partial \sigma_k^2}{\partial \textbf{$\omega$}} = 2 \textbf{$\Sigma$}_k \textbf{$\omega$},\; \frac{\partial \sigma_k^2}{\partial \omega_0} = 0,\; \frac{\partial m_k}{\partial \textbf{$\omega$}} = \textbf{$\mu$}_k,\; \frac{\partial m_k}{\partial \omega_0} = 1 $$なので
評価関数の微分に代入すれば $$ 2\left(\frac{\partial h}{\partial \sigma_1^2} \textbf{$\Sigma$}_1 + \frac{\partial h}{\partial \sigma_2^2} \textbf{$\Sigma$}_2\right) \textbf{$\omega$} = \frac{\partial h}{\partial m_1} \textbf{$\mu$}_1 + \frac{\partial h}{\partial m_2} \textbf{$\mu$}_2 \\ \frac{\partial h}{\partial m_1} + \frac{\partial h}{\partial m_2} = 0 $$
$$ s = \frac{\frac{\partial h}{\partial \sigma_1^2}} {\frac{\partial h}{\partial \sigma_1^2} + \frac{\partial h}{\partial \sigma_2^2}} $$と定義して $$ 2\left(\frac{\partial h}{\partial \sigma_1^2} \textbf{$\Sigma$}_1 + \frac{\partial h}{\partial \sigma_2^2} \textbf{$\Sigma$}_2\right) \textbf{$\omega$} = \frac{\partial h}{\partial m_1} \textbf{$\mu$}_1 + \frac{\partial h}{\partial m_2} \textbf{$\mu$}_2 $$を整理すると $$ 2\left(\frac{\partial h}{\partial \sigma_1^2} + \frac{\partial h}{\partial \sigma_2^2}\right) (s \textbf{$\Sigma$}_1 + (1 - s)\textbf{$\Sigma$}_2) \textbf{$\omega$} = \frac{\partial h}{\partial m_1} (\textbf{$\mu$}_2 - \textbf{$\mu$}_1) $$より、最適な$\textbf{$\omega$}$は、 スカラー項を無視すれば $$ \textbf{$\omega$} = (s \textbf{$\Sigma$}_1 + (1 - s) \textbf{$\Sigma$}_2)^{-1} (\textbf{$\mu$}_2 - \textbf{$\mu$}_1) $$ となる
評価関数をクラス間分散とクラス内分散の比 $$ h = \frac{P(C_1)(m_1 - \bar{m})^2 + P(C_2)(m_2 - \bar{m})^2}{P(C_1)\sigma_1^2 + P(C_2)\sigma_2^2} $$ で定義した判別関数を判別分析法という($\bar{m}$は全データの平均)
この場合、 $$ \frac{\partial h}{\partial \sigma_k^2} = \frac{P(C_k)(P(C_1)(m_1 - \bar{m})^2 + P(C_2)(m_2 - \bar{m})^2)} {(P(C_1)\sigma_1^2 + P(C_2)\sigma_2^2)^2} $$を $ s = \frac{\frac{\partial h}{\partial \sigma_1^2}} {\frac{\partial h}{\partial \sigma_1^2} + \frac{\partial h}{\partial \sigma_2^2}} $ に代入すると$s = P(C_1)$なので、最適な$\textbf{$\omega$}$は $$ \textbf{$\omega$} = (P(C_1) \textbf{$\Sigma$}_1 + P(C_2) \textbf{$\Sigma$}_2)^{-1} (\textbf{$\mu$}_2 - \textbf{$\mu$}_1) $$
$$ \frac{\partial h}{\partial m_k} = \frac{2 P(C_k)(m_k - \bar{m})}{P(C_1)\sigma_1^2 + P(C_2)\sigma_2^2} $$と $$ \frac{\partial h}{\partial m_1} + \frac{\partial h}{\partial m_2} = 0 $$より $$ P(C_1)(m_1 - \bar{m}) + P(C_2)(m_2 - \bar{m}) = 0 $$なので、$m_k = \textbf{$\omega$}^T \textbf{$\mu$}_k + \omega_0$ を代入して整理すれば、最適なバイアス項が得られる $$ \omega_0 = -\textbf{$\omega$}(P(C_1)\textbf{$\mu$}_1 + P(C_2)\textbf{$\mu$}_2) $$
多クラス問題の場合は識別境界を計算できない
各クラスのデータ数を$N_k\;(k=1,\ldots,K)$, クラス内変動を $$ {\bf S}_k = \sum_{i \in C_k} ({\bf x}_i - \textbf{$\mu$}_k) ({\bf x}_i - \textbf{$\mu$}_k)^T \\ \textbf{$\mu$}_k = \frac{1}{N_k} \sum_{i \in C_k} {\bf x}_i \\ {\bf S}_W = \sum_{k = 1}^K {\bf S}_k $$ とすると、全データの平均$\textbf{$\mu$}$は $$ \textbf{$\mu$} = \frac{1}{N} \sum_{i = 1}^N {\bf x}_i = \frac{1}{N} \sum_{k = 1}^K N_k \textbf{$\mu$}_k \\ N = N_1 + \cdots + N_K $$
全平均からの全データの変動の和を全変動${\bf S}_T$という $$ \begin{align} {\bf S}_T & = \sum_{i = 1}^N ({\bf x}_i - \textbf{$\mu$}) ({\bf x}_i - \textbf{$\mu$})^T \\ & = \sum_{k = 1}^K \sum_{i \in C_k} ({\bf x}_i - \textbf{$\mu$}_k + \textbf{$\mu$}_k - \textbf{$\mu$}) ({\bf x}_i - \textbf{$\mu$}_k + \textbf{$\mu$}_k - \textbf{$\mu$})^T \\ & = \sum_{k = 1}^K \sum_{i \in C_k} ({\bf x}_i - \textbf{$\mu$}_k) ({\bf x}_i - \textbf{$\mu$}_k)^T + \sum_{k = 1}^K N_k (\textbf{$\mu$}_k - \textbf{$\mu$}) (\textbf{$\mu$}_k - \textbf{$\mu$})^T \\ & = {\bf S}_W + \sum_{k = 1}^K N_k (\textbf{$\mu$}_k - \textbf{$\mu$}) (\textbf{$\mu$}_k - \textbf{$\mu$})^T \end{align} $$
最後の項から、クラス間変動${\bf S}_B$を定義する $$ {\bf S}_B = \sum_{k = 1}^K N_k (\textbf{$\mu$}_k - \textbf{$\mu$}) (\textbf{$\mu$}_k - \textbf{$\mu$})^T $$
各クラスの平均ベクトル${\bf m}_k$と全平均ベクトル${\bf m}$は $$ {\bf m}_k = \frac{1}{N_k} \sum_{i \in C_k} = \frac{1}{N_k} \sum_{i \in C_k} {\bf W}^T {\bf x}_i = {\bf W}^T \textbf{$\mu$}_k \\ {\bf m} = \frac{1}{N} \sum_{k = 1}^K N_k {\bf m}_k = \frac{1}{N} \sum_{k = 1}^K N_k {\bf W}^T \textbf{$\mu$}_k = {\bf W}^T \textbf{$\mu$} $$なので
$$ \begin{align} \widetilde{{\bf S}}_W & = \sum_{k = 1}^K \sum_{i \in C_k}({\bf y}_i - {\bf m}_k) ({\bf y}_i - {\bf m}_k)^T \\ & = \sum_{k = 1}^K \sum_{i \in C_k} {\bf W}^T ({\bf x}_i - \textbf{$\mu$}_k) \{ {\bf W}^T ({\bf x}_i - \textbf{$\mu$}_k)\}^T \\ & = \sum_{k = 1}^K \sum_{i \in C_k} {\bf W}^T ({\bf x}_i - \textbf{$\mu$}_k) ({\bf x}_i - \textbf{$\mu$}_k)^T {\bf W} = {\bf W}^T {\bf S}_W {\bf W} \end{align} $$
$$ \begin{align} \widetilde{{\bf S}}_B & = \sum_{k = 1}^K N_k ({\bf m}_k - {\bf m}) ({\bf m}_k - {\bf m})^T \\ & = \sum_{k = 1}^K N_k {\bf W}^T (\textbf{$\mu$}_k - \textbf{$\mu$}) \{ {\bf W}^T (\textbf{$\mu$}_k - \textbf{$\mu$}) \}^T \\ & = \sum_{k = 1}^K N_k {\bf W}^T (\textbf{$\mu$}_k - \textbf{$\mu$}) (\textbf{$\mu$}_k - \textbf{$\mu$})^T {\bf W} = {\bf W}^T {\bf S}_B {\bf W} \end{align} $$
最適な写像行列${\bf W}$を求めるための基準は、クラス間変動行列$\widetilde{{\bf S}}_B$と クラス内変動行列$\widetilde{{\bf S}}_W$の比を最大化すること
行列の比なので、スカラーに変換する必要があり、一つの方法が $$ J({\bf W}) = Tr({\bf S}_W^{-1} {\bf S}_B) = Tr(({\bf W}^T {\bf S}_W {\bf W})^{-1} {\bf W}^T {\bf S}_B {\bf W})$$ を最大化すること
ロジスティック回帰
線形識別関数$y = \textbf{$\omega$}^T {\bf x}$は、データが識別境界から離れるに従って、関数値が線形に上昇し続ける
ロジスティック回帰では、関数値を区間$(0, 1)$に制限し、確率的な解釈を可能にする
回帰という名前だが識別が目的
クラス$C_1$の事後確率$P(C_1|{\bf x})$は $$ P(C_1|{\bf x}) = \frac{p({\bf x}|C_1) P(C_1)}{p({\bf x}|C_1) P(C_1) + p({\bf x}|C_2) P(C_2)} $$
このとき、$ a = ln \frac{p({\bf x}|C_1)P(C_1)}{p({\bf x}|C_2)P(C_2)} $とおけば $$ P(C_1|{\bf x}) = \frac{1}{1 + \exp(-a)} = \sigma(a) $$ と表すことができる
$\sigma(a)$をロジスティック関数と呼ぶ
ロジスティック関数$y = \sigma()$は無限区間$(-\infty, \infty)$を区間$(0, 1)$に写像する、S字型をした圧縮関数
また、以下のような対称性を示す $$ \sigma(-a) = 1 - \sigma(a) $$
ロジスティック関数の逆関数をロジット関数といい $$ a = ln \left( \frac{\sigma(a)}{1 - \sigma(a)} \right) = ln \frac{P(C_1|{\bf x})}{P(C_2|{\bf x})} $$ 最後の項の事後確率の比をオッズ、その対数をログオッズという
ロジスティック回帰モデルは、事象の有無を$\{0, 1\}$の2値で表し、事象の生起確率をロジスティック関数で表す
$N$個の値$ \hat{{\bf x}} = (x1, \ldots , x_N)^T $を観測した時、事象が生起する確率を以下の式で表す $$ p(1|x_1, \ldots , x_N) = f({\bf x}) = \frac{1}{1 + \exp(-(\omega_0 + \omega_1 x_1 + \cdots + \omega_N x_N))} $$
$ \textbf{$\omega$} = (\omega_0, \omega_1, \ldots , \omega_N)^T,\;\; {\bf x} = (1, \hat{{\bf x}}^T)^T, \;\; a = \textbf{$\omega$}^T {\bf x} $ とすれば、 $f({\bf x})$はロジスティック関数となり、以下のように表せる $$ f({\bf x}) = \sigma(a) = \frac{1}{1 + \exp(-a)} = \frac{\exp\;a}{1 + \exp\;a} $$
$ f({\bf x}) = \sigma(a) = \frac{1}{1 + \exp(-a)} = \frac{\exp\;a}{1 + \exp\;a} $は非線形なので、学習データの線形関数$a$を ロジスティック関数で非線形変換したモデルで事象を表現している
線形関数を非線形変換しても識別境界は超平面となるので、ロジスティック回帰モデルは一般化線形モデルの1つである
ロジット関数は $$ a = ln \frac{p(1|{\bf x})}{1 - p(1|{\bf x})} = \textbf{$\omega$}^T {\bf x} $$で、オッズは $$ \frac{p(1|{\bf x})}{1 - p(1|{\bf x})} = \frac{p(1|{\bf x})}{p(0|{\bf x})} = \exp(\textbf{$\omega$}^T {\bf x}) $$
${\bf x}$の中の$x_1$が1増えた状態$\widetilde{\bf x} = (1, (x_1 + 1), x_2, \ldots, x_N)$を考える
${\bf x}$とのオッズ比は $$ \frac{\frac{p(1|\widetilde{\bf x})}{1 - p(1|\widetilde{\bf x})}}{\frac{p(1 | {\bf x})}{1 - p(1 | {\bf x})}} = \frac{\exp(\omega_0 + \omega_1(x_1 + 1) + \omega_2 x_2 + \cdots + \omega_N x_N)} {\exp(\omega_0 + \omega_1 x_1 + \omega_2 x_2 + \cdots + \omega_N x_N)} = \exp\;\omega_1$$
オッズ比の効用
| 条件A | 条件B | ||
|---|---|---|---|
| 環境1 | 成功 | 0.9 | 0.99 |
| 失敗 | 0.1 | 0.01 | |
| 環境2 | 成功 | 0.5 | 0.55 |
| 失敗 | 0.5 | 0.45 | |
環境1, 2でそれぞれ条件Aから条件Bに変えた時の成功の増加割合は$P(B)/P(A) = 1.1$で等しい
しかし、0.9から0.99への上昇と0.5から0.55への上昇には質的な違いがある
オッズ比$\frac{P(B)}{1 - P(B)} / \frac{P(A)}{1 - P(A)}$を求めると、環境1は11、環境2は1.22となる
パラメータの最尤推定
モデルの出力を確率変数$t$、$t$が1となる確率を$p(t = 1) = \alpha$、0となる確率を$p(t = 0) = 1 - \alpha$で表すと、 確率変数$t$はパラメータ$\alpha$を持つベルヌーイ試行 $$ f(t|\alpha) = \alpha^t(1 - \alpha)^{1 - t} \;\; (t = 0, 1) $$に従うので、$N$回の試行に基づく尤度関数は $$ L(\alpha_1, \ldots, \alpha_N) = \prod_{i = 1}^N f(t_i | \alpha_i) = \prod_{i = 1}^N \alpha_i^{t_i} (1 - \alpha_i)^{1 - t_i} $$ となり、 負の対数尤度関数は $$ \begin{align} \cal{L}(\alpha_1, \ldots , \alpha_N) & = - \ln L(\alpha_1, \ldots , \alpha_N) \\ & = - \sum_{i = 1}^N (t_i \ln \alpha_i + (1 - t_i) \ln(1 - \alpha_i)) \end{align}$$
$$ \alpha_i = \sigma({\bf x}_i) = \frac{\exp (\textbf{$\omega$}^T {\bf x}_i)}{1 + \exp(\textbf{$\omega$} {\bf x}_i)} $$ を負の対数尤度関数に代入すると $$ \begin{align} \cal{L}(\alpha_1, \ldots , \alpha_N) & = \cal{L}(\textbf{$\omega$}) \\ & = s \sum_{i = 1}^N (t_i \textbf{$\omega$}^T {\bf x}_i - \ln(1 + \exp(\textbf{$\omega$}^T {\bf x}_i))) \end{align} $$ この交差エントロピー型誤差関数を最小にするパラメータ$\textbf{$\omega$}$を得るために、対数尤度関数を$\textbf{$\omega$}$で 微分すればよい
対数尤度関数を$\textbf{$\omega$}$で微分すると $$ \begin{align} \frac{\partial \cal{L}(\textbf{$\omega$})}{\partial \textbf{$\omega$}} & = - \sum_{i = 1}^N \left( t_i {\bf x}_i - \frac{{\bf x}_i \exp(\textbf{$\omega$}^T {\bf x}_i)}{1 + \exp(\textbf{$\omega$}^T {\bf x}_i)} \right) \\ & = \sum_{i = 1}^N {\bf x}_i (\alpha_i - t_i) \end{align} $$となり、この式が0となる$\textbf{$\omega$}$が解である
しかし、解析的に解を求めることは出来ないので、最急降下法やニュートン-ラフソン法を用いる
多クラスへ拡張するためには、各クラスごとに線形変換 $$ a_k = \textbf{$\omega$}_k^T {\bf x}\;\;\;(k=1, \ldots , K) $$ を求め、事後確率を $$ P(C_k|{\bf x}) = \pi_k({\bf x}) = \frac{\exp a_k}{\sum_{j = 1}^K \exp a_j} $$ で計算して、最大事後確率を与えるクラスに分類する
この関数をソフトマックス関数という
クラス数$K$、学習データ${\bf X} = ({\bf x}_1, \ldots , {\bf x}_K)^T$、教師データ${\bf T} = ({\bf t}_1, \ldots , {\bf t}_N)^T$ とすると、尤度関数は $$ p({\bf T}|\textbf{$\omega$}_1, \cdots , \textbf{$\omega$}_K) = \prod_{i=1}^N \prod_{k=1}^K P(C_k|{\bf x}_i)^{t_{ik}} = \prod_{i=1}^N \prod_{k=1}^K \pi_{ik}^{t_{ik}} \\ \pi_{ik} = \frac{\exp a_{ik}}{\sum_{j = 1}^K \exp a_{ij}},\;\;\; a_{ij} = \textbf{$\omega$}_j^T {\bf x}_i $$
事後確率をソフトマックス関数でモデル化した場合の負の対数尤度関数は $$ \begin{align} E(\textbf{$\omega$}_i, \cdots , \textbf{$\omega$}_K) & = - \ln p({\bf T}|\textbf{$\omega$}_i, \cdots , \textbf{$\omega$}_K) \\ & = - \sum_{i = 1}^N \sum_{k = 1}^K t_{ik} \pi_{ik} \end{align} $$となり、各$\textbf{$\omega$}_j$の最尤推定は 評価関数を$\textbf{$\omega$}_j$で微分して0とおけば求められる