はじめてのパターン認識
5章
Created by 2GMon
話の流れ
- kNN法について
- kNN法の誤り率とベイズ誤り率の関係
- kNN法の計算量緩和策
最近傍法
- 入力データと全ての学習データの距離比較を行い、一番近い学習データのクラスに識別する方法
- 学習データが多ければ精度はかなり良いが、計算時間がかかる
- 一番近い学習データの代わりに近いk個のデータを選び、一番多いクラスに識別するkNN法もある
- $K$個のクラスを$\Omega = \{ C_1, \ldots , C_K \}$
- $i$番目のクラスの学習データ数を$N(i)$
- 学習データの集合を$S_i = \{ {\bf x}_1^{(i)}, \ldots , {\bf x}_{N(i)}^{(i)}\}$
- ${\bf x}$と${\bf x}_j^{(i)}$のユークリッド距離を$d({\bf x}, {\bf x}_j^{(i)}) = || {\bf x} - {\bf x}_j^{(i)}||$
とした場合
- 学習データの集合を$T_N = \{ {\bf x}_i , \ldots , {\bf x}_N \}$
- クラスの集合を$\Omega = \{ C_1, \ldots , C_K \}$
- $i$番目のデータが所属するクラスを$\omega_i \in \Omega$
- 入力${\bf x}$に最も近い$k$個の学習データの集合を$k({\bf x}) = \{ {\bf x}_{i1} , \ldots , {\bf x}_{ik} \}$
- $k$個の学習データのうちクラス$j$に所属するデータの数を$k_j\; (k = k_1 + \cdots + k_K)$
とした場合
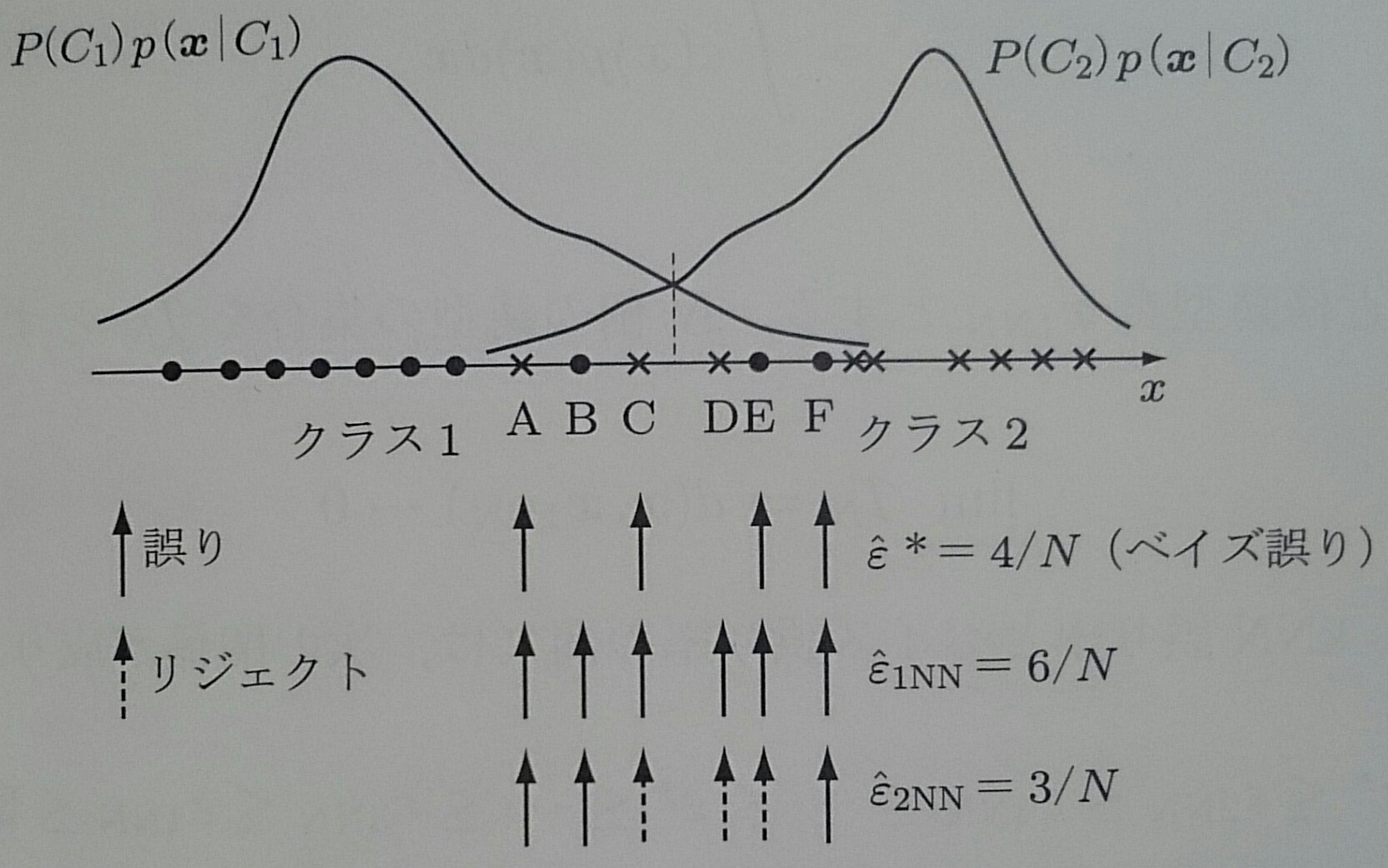
上図の場合は、$\hat{\epsilon}_{2NN} \leq \hat{\epsilon}^* \leq \hat{\epsilon}_{1NN}$が成り立っている
2クラス問題の場合、条件付きベイズ誤り率は事後確率の小さい方(3章) $$ \epsilon({\bf x}) = min[P(C_1|{\bf x}), P(C_2|{\bf x})]$$
ベイズ誤り率は条件付きベイズ誤り率の期待値 $$ \epsilon^* = \int \epsilon({\bf x})p({\bf x}) d{\bf x} $$
入力${\bf x}$に最も近いデータを${\bf x}_{1NN}$とし、$N$個のデータの集合を$T_N$としたときに漸近仮定 $$ \displaystyle \lim_{N \to \infty} T_N => d({\bf x}, {\bf x}_{1NN}) \to 0 $$ が成り立てば、kNN誤り率とベイズ誤り率の間には以下の関係が成り立つ $$ \frac{1}{2} \epsilon^* \leq \epsilon_{2NN} \leq \epsilon_{4NN} \leq \cdots \leq \epsilon^* \leq \cdots \leq \epsilon_{3NN} \leq \epsilon_{1NN} \leq 2 \epsilon^* $$
1NNの場合の証明
まず、1NN誤り率の上限を求める
1NNの場合、誤り率は $$ \begin{align} r_1({\bf x}, {\bf x}_{1nn}) = & P({\bf x} \in C_1, {\bf x}_{1NN} \in C_2 | {\bf x}, {\bf x}_{1NN}) \\ & + P({\bf x} \in C_2, {\bf x}_{1NN} \in C_1 | {\bf x}, {\bf x}_{1NN}) \\ = & P(C_1 | {\bf x}) P(C_2 | {\bf x}_{1NN}) + P(C_2 | {\bf x}) P(C_1 | {\bf x}_{1NN}) \end{align}$$
漸近仮定が成り立てば${\bf x}$と${\bf x}_{1NN}$の区別はなくなるので $$ \displaystyle \begin{align} r_1({\bf x}) = & \lim_{N \to \infty} r_1({\bf x}, {\bf x}_{1NN}) = 2P(C_1 | {\bf x})P(C_2 | {\bf x}) \\ = & 2P(C_1 | {\bf x})(1 - P(C_1 | {\bf x})) = 2(1 - P(C_2 | {\bf x}))P(C_2 | {\bf x}) \\ = & 2 \epsilon({\bf x}) (1 - \epsilon({\bf x})) \end{align} $$
よって、1NNの誤り率の期待値は $$ \begin{align} \epsilon_{1NN} = & \int 2 \epsilon({\bf x})(1 - \epsilon({\bf x})) p({\bf x}) d{\bf x} \\ = & 2 \int \epsilon({\bf x}) p({\bf x}) d{\bf x} - 2 \int \epsilon^2({\bf x}) p({\bf x}) d{\bf x} \end{align}$$
第1項はベイズ誤り率$\epsilon^*$の2倍で、第2項は$\geq 0$なので $\epsilon_{1NN} \leq 2\epsilon^*$ となり、 1NN誤り率の上限はベイズ誤り率の2倍に抑えられる
次に、1NN誤り率の下限を求める
ベイズ誤り率は $$ \begin{align} \epsilon^* = & \int min[P(C_1 | {\bf x}), P(C_2 | {\bf x})] p({\bf x}) d{\bf x} \\ = & \int min[p({\bf x} | C_1) P(C_1), p({\bf x} | C_2) P(C_2)] d{\bf x} \end{align}$$
1NN誤り率は $$ \begin{align} \epsilon_{1NN} = & \int 2P(C_1 | {\bf x}) P(C_2 | {\bf x}) p({\bf x}) d{\bf x} \\ = & \int 2 \frac{p({\bf x} | C_1) P(C_1) p({\bf x} | C_2) P(C_2)}{p({\bf x}} d{\bf x} \\ = & \int 2 \frac{p({\bf x} | C_1) P(C_1) p({\bf x} | C_2) P(C_2)}{p({\bf x} | C_1) P(C_1) + p({\bf x} | C_2) P(C_2)} d{\bf x} \end{align}$$
$$ \begin{array}{ll} a > b であれば\;\; & b < \frac{2}{1 + b/a}b = 2 \frac{ab}{a + b} \\ a < b であれば\;\; & a < \frac{2}{1 + a/b}a = 2 \frac{ab}{a + b} \end{array} $$ なので $$ min[a, b] \leq 2 \frac{ab}{a + b} $$ より
$a = p({\bf x} | C_1) P(C_1), b = p({\bf x} | C_2) P(C_2)$とおくと $ \epsilon^* \leq \epsilon_{1NN} $
以上より $$ \epsilon^* \leq \epsilon_{1NN} \leq 2 \epsilon^* $$
漸近仮定が成り立つ場合は以下の関係が成り立つ $$ \frac{1}{2} \epsilon^* \leq \epsilon_{2NN} \leq \epsilon_{4NN} \leq \cdots \leq \epsilon^* \leq \cdots \leq \epsilon_{3NN} \leq \epsilon_{1NN} \leq 2 \epsilon^* $$
次は、漸近仮定が成り立つのかを考える
$d$次元空間において、あるデータ${\bf x}$から距離$a$以内にあるデータの数を考える
データが一様に分布しているとすると距離$a$以内にあるデータの数は、半径$a$の$d$次元超球の体積に比例する
$d$次元単位超球の表面積$S_d$は $$ S_d = \frac{2 \pi^{1/2}}{\Gamma (d / 2)},\;\; \Gamma (x) = \int_0^\infty u^{x - 1} e^{-u} du $$
半径$a$の超球の表面積と体積は $$ S_d(a) = S_d * a^{d-1} \\ V_d(a) = \int_0^a S_d x^{d - 1} dx = \frac{S_d a^d}{d} $$
半径1の超球の体積と、厚さ$\epsilon$の殻の体積比を求めると以下のようになる $$ \frac{V_d(1) - V_d(1- \epsilon)}{V_d(1)} = 1 - (1 - \epsilon)^d \xrightarrow{d \to \infty} 1 $$
次元が大きくなると体積比は1に近づくので、全体積のうち厚さ$\epsilon$の殻が占める割合が大きくなる。 よって、あるデータ${\bf x}$から見ると、他のデータは${\bf x}$の近傍にはなく、同じような距離にあることがわかる
次元が大きい時は漸近仮定が成り立たない
$d$次元の$k$クラス問題で、各クラスの学習データはそれぞれ$M$個あるとする
kNN法では入力データ${\bf x}$が与えられた時、全ての学習データとのユークリッド距離を計算するので $O(KMd)$となる。さらに距離をソートするので$O(KMlog(KM))$となり、kNN法は実時間認識には向いていない

1NNの場合、BやDは本来正しい領域に存在しているのに、A,CやE,Fに影響されて誤ってしまうので、ベイズ誤り率よりも高い確率で誤りが発生する
正しくないクラスの領域に存在している学習データを削除すれば防げるが、正確なベイズ境界はわからない
誤って識別されたデータを全て削除して構成された誤り削除集合を用いて識別を行う、Edited kNN法がある
Edited kNN法の誤り率はベイズ誤り率と等しくはならないが、ベイズ誤り率と1NN誤り率の間になることが知られている
kNN法はベイズ境界付近のデータが重要なので、識別に寄与しないデータを学習データから削除するCondensed kNN法がある
識別に寄与しないデータは $\epsilon({\bf x}) = min[P(C_1|{\bf x}), P(C_2|{\bf x})]$ を小さくするように決める
学習データをクラスタリングなどを用いて重なりのない集合に分割し、木構造に組織化する
集合の平均ベクトルと入力データの距離を計算することで、遠いクラスタに属するデータそれぞれとの距離計さんを省くことができる
これを限定法といい、効率的に探索できるかは木構造による
近似解を高速に求める近似最近傍探索がある
学習データの集合を$P=\{{\bf x}_i\}\; (i = 1, \ldots , N)$とし、入力データ${\bf q}$に対する最近傍解${\bf x}^*$の $\epsilon$近似解 ${\bf x}$ を $d({\bf q}, {\bf x}) \leq (1 + \epsilon)d({\bf q}, {\bf x}^*)$を満たす解${\bf x} \in P$として定義する
$d({\bf q}, {\bf x})$の値は一般的にわからないので、何らかの形で近似解が$\epsilon$近似となることを保証する必要がある
$\epsilon$近似を保証できる時間的・空間的制約の少ない領域分割法が必要で、BBD木やリングカバー木などが提案されている